Objectes multimèdia amb l’etiqueta: Geometria
Resultats de la cerca
Indecibilitat, complexitat i caos: dels conjunts de Cantor a les màquines de Turing i més enllà
Accés obert
4 de maig 2022
The speaker of the IMTech Colloquium will be Eva Miranda (UPC), a leading figure in Differential Geometry, Mathematical Physics and Dynamical Systems
Les varietats invariants i el seu paper en els sistemes dinàmics: de les òrbites dels cometes a les ones cerebrals
Accés obert
16 de març 2022
Maria Teresa Martínez-Seara Alonso en el Cicle de Xerrades Panoràmiques sobre temes de recerca d'actualitat adreçades a estudiants i joves investigadors
¿Por qué le llaman Física cuando quieren decir Geometría?. Jornada Hilbert (Curs 2017-2018)
Accés obert
28 de febr. 2018
Clara Grima (Sevilla,1971) es doctora en Matemáticas y profesora titular del Departamento de Matemática Aplicada I de la Universidad de Sevilla. Miembro del grupo de investigación en Matemática Discreta y autora, entre otras publicaciones científicas, del libro "Computational Geometry on Surfaces" (Springer, 2001) (con Alberto Márquez).
Desde 2010 compagina su labor de investigación con la divulgación de las matemáticas en casi cualquier formato posible (blogs, prensa, libros, radio, televisión, Youtube, conferencias, teatro...). Es la presidenta de la comisión de divulgación de la Real Sociedad Matemática Española y ha recibido el premio COSCE 2017 (otorgado por la Confederación de Sociedades Científicas Españolas) a la difusión de la Ciencia.
Junto a cuatro compañeras más de la Universidad de Sevilla, recibió en 2016 el premio Equit@t de la Universitat Oberta de Catalunya por la obra de teatro "Científicas: pasado, presente y futuro".
Está empeñada en enseñar matemáticas a todo el mundo y se lo pasa muy bien en el intento. O eso parece.
Decía David Hilbert que "la física es demasiado difícil como para dejársela a los físicos". En esta charla vamos a presentar al Hilbert preocupado por la física puesto que le tocó vivir la que sin duda ha sido, hasta la fecha, la época más excitante de dicha disciplina. La aparición de la Relatividad, Especial y General, así como de la Cuántica, a principios del siglo XX convulsionaron nuestra forma de entender el universo. Pero no solo eso, también supusieron la introducción en las ciencias físicas de ramas matemáticas que le eran ajenas. Campos como la geometría diferencial, el análisis funcional o la teoría de grupos comenzaron a ser elementos indispensables para afrontar el estudio de los procesos físicos. Hilbert no solo no fue insensible a estas corrientes y nuevas teorías sino que participó de manera activa y decisiva. En esta charla daremos unas pinceladas de las aportaciones de Hilbert a la física centrándonos en su trabajo en Relatividad General. Esto nos permitirá ver cómo encaja la física en el esquema conceptual que Hilbert había desarrollado en toda su vida matemática, conocer un par de anécdotas de su relación con Albert Einstein y reivindicar a una gran dama de las matemáticas: Emmy Noether.
Desde 2010 compagina su labor de investigación con la divulgación de las matemáticas en casi cualquier formato posible (blogs, prensa, libros, radio, televisión, Youtube, conferencias, teatro...). Es la presidenta de la comisión de divulgación de la Real Sociedad Matemática Española y ha recibido el premio COSCE 2017 (otorgado por la Confederación de Sociedades Científicas Españolas) a la difusión de la Ciencia.
Junto a cuatro compañeras más de la Universidad de Sevilla, recibió en 2016 el premio Equit@t de la Universitat Oberta de Catalunya por la obra de teatro "Científicas: pasado, presente y futuro".
Está empeñada en enseñar matemáticas a todo el mundo y se lo pasa muy bien en el intento. O eso parece.
Decía David Hilbert que "la física es demasiado difícil como para dejársela a los físicos". En esta charla vamos a presentar al Hilbert preocupado por la física puesto que le tocó vivir la que sin duda ha sido, hasta la fecha, la época más excitante de dicha disciplina. La aparición de la Relatividad, Especial y General, así como de la Cuántica, a principios del siglo XX convulsionaron nuestra forma de entender el universo. Pero no solo eso, también supusieron la introducción en las ciencias físicas de ramas matemáticas que le eran ajenas. Campos como la geometría diferencial, el análisis funcional o la teoría de grupos comenzaron a ser elementos indispensables para afrontar el estudio de los procesos físicos. Hilbert no solo no fue insensible a estas corrientes y nuevas teorías sino que participó de manera activa y decisiva. En esta charla daremos unas pinceladas de las aportaciones de Hilbert a la física centrándonos en su trabajo en Relatividad General. Esto nos permitirá ver cómo encaja la física en el esquema conceptual que Hilbert había desarrollado en toda su vida matemática, conocer un par de anécdotas de su relación con Albert Einstein y reivindicar a una gran dama de las matemáticas: Emmy Noether.
Hyper-Kähler geometry
Accés obert
29 de nov. 2017
La professora Claire Voisin ocupa des de l'any 2016 la càtedra de geometria algebraica del Còllege de France. La seva àrea de recerca és la geometria algebraica, i més particularment la teoria de Hodge. En aquesta àrea ha realitzat múltiples contribucions, incloent la refutació de la conjectura de Kodaira sobre deformacions de varietats de Kähler, i la prova que la generalització de la conjectura de Hodge per varietats de Kähler compactes és falsa.
La professora Voisin ha rebut múltiples reconeixements per les seves contribucions a la geometria algebraica, incloent ser conferenciant convidada a l'ICM de Zürich l'any 1994 (Secció Geometria Algebraica) i conferenciant plenària a l'ICM de Hyderabad (2014). Ha rebut les medalles de bronze, plata i or del CNRS (l'última d'elles l'any 2016), el premi Heinz Hopf, el premi Clay en recerca matemàtica i més recentment, el 2017, el premi Shaw, denominat com els "Nobel asiàtics", compartit amb el matemàtic János Kollár.
Kähler geometry is a natural extension of complex projective geometry where the tools of Hodge theory are still available and allow to study the link between topology and complex geometry.
The simplest examples of projective complex manifolds deforming to non-projective ones are the abelian varieties (complex tori) of dimension at least 2. The subject of the lecture will be hyper-Kähler (or quaternionic) manifolds, which also share this property. This geometry was discovered by Beauville on the basis of Yau's fundamental work on existence of Kähler-Einstein metrics. Although this geometry may seem extremely restricted, there are many (families of) examples, all built via algebraic geometry.
La professora Voisin ha rebut múltiples reconeixements per les seves contribucions a la geometria algebraica, incloent ser conferenciant convidada a l'ICM de Zürich l'any 1994 (Secció Geometria Algebraica) i conferenciant plenària a l'ICM de Hyderabad (2014). Ha rebut les medalles de bronze, plata i or del CNRS (l'última d'elles l'any 2016), el premi Heinz Hopf, el premi Clay en recerca matemàtica i més recentment, el 2017, el premi Shaw, denominat com els "Nobel asiàtics", compartit amb el matemàtic János Kollár.
Kähler geometry is a natural extension of complex projective geometry where the tools of Hodge theory are still available and allow to study the link between topology and complex geometry.
The simplest examples of projective complex manifolds deforming to non-projective ones are the abelian varieties (complex tori) of dimension at least 2. The subject of the lecture will be hyper-Kähler (or quaternionic) manifolds, which also share this property. This geometry was discovered by Beauville on the basis of Yau's fundamental work on existence of Kähler-Einstein metrics. Although this geometry may seem extremely restricted, there are many (families of) examples, all built via algebraic geometry.
Perspectiva cónica (CO), ejercicio: Perspectiva cónica de una figura en forma de L
Accés obert
17 de febr. 2016
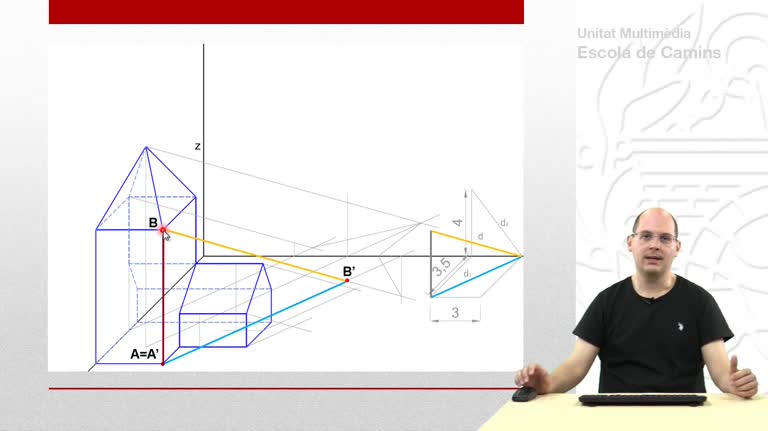
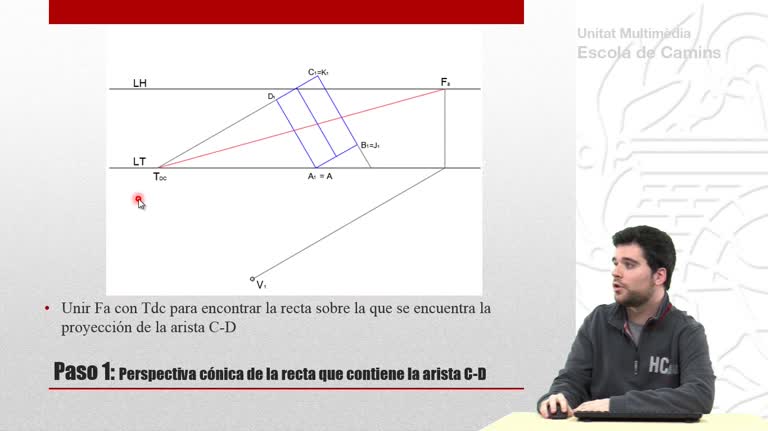
Perspectiva cónica de una figura en forma de L. Se utiliza el método de las prolongaciones.
Perspectiva cónica (CO), ejercicio: Tetraedro, método de las prolongaciones
Accés obert
1 de febr. 2016
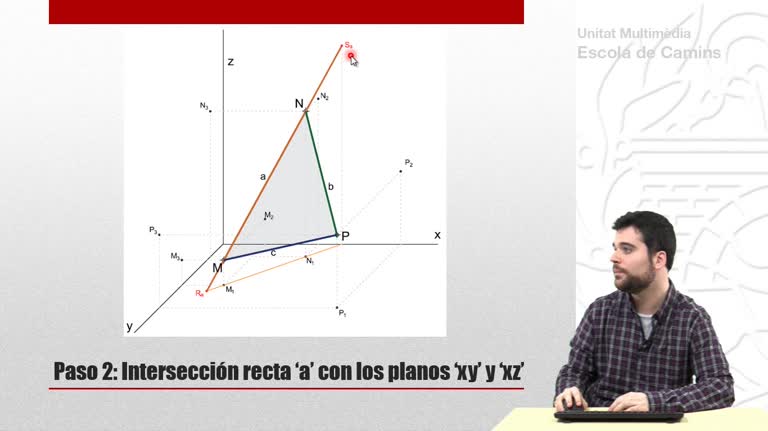
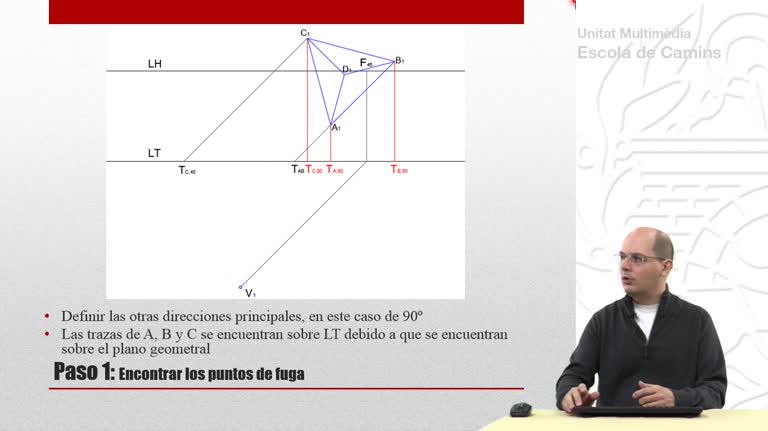
Perspectiva cónica de un tetraedro que descansa sobre el plano geometral. En esta primera parte se utiliza el método de las prolongaciones.
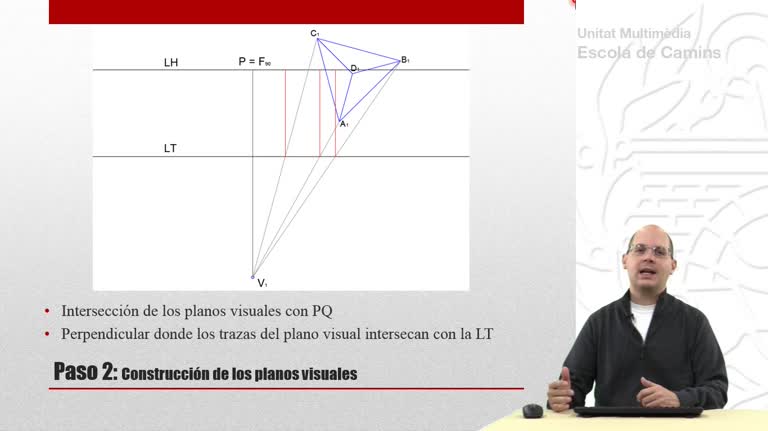
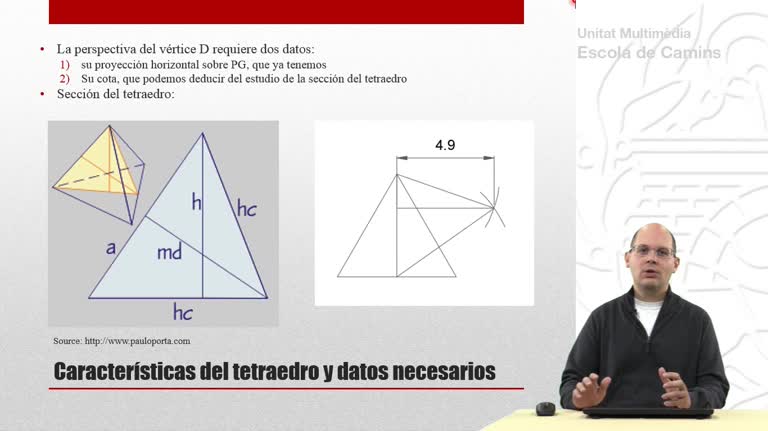
Perspectiva cónica (CO), ejercicio: Tetraedro, rectas de punta y planos visuales
Accés obert
1 de febr. 2016
Perspectiva cónica de un tetraedro que descansa sobre el plano geometral. En esta segunda parte se utilizan planos visuales y rectas de punta.
Perspectiva cónica (CO), ejercicio: Tetraedro, cota del punto de vista nula
Accés obert
1 de febr. 2016
Perspectiva cónica de un tetraedro que descansa sobre el plano geometral. El punto de vista tiene cota nula, con lo cual la planta del tetraedro se ve de perfil.
Geometría II
Accés obert
19 de gen. 2016
Este vídeo forma parte del MOOC "El lenguaje de la Ingeniería", módulo de Matemáticas. https://mooc.upc.edu/