Objectes multimèdia amb l’etiqueta: Centres docents
Resultats de la cerca
Jornada I+D+i en Ingeniería Civil 2008 (2/2)
Accés obert
21 de nov. 2008
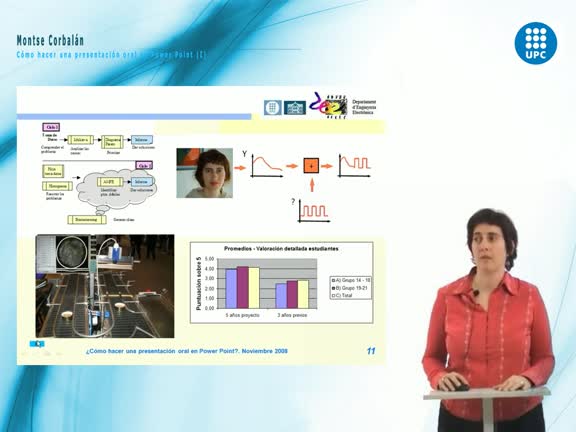
Presentación de los proyectos de investigación que lleva a cabo la Escuela de Caminos realizada durante la "Jornada I+D+i en Ingeniería Civil” que se produjo el día 21 de noviembre en la Sala de Actos de la Escuela de Ingenieros de Caminos, Canales y Puertos de Barcelona.
Ingeniería del Terreno por Antoni Gens
Ingeniería del Agua por Josep Dolz
Ing. de Estructuras y Construcción por Antoni Marí
Ingeniería del Transporte y Territorio por Andrés López Pita
Ingeniería Computacional por Eugenio Oñate
Medio Ambiente y Sostenibilidad por Xavier Sánchez-Vila
Ingeniería del Terreno por Antoni Gens
Ingeniería del Agua por Josep Dolz
Ing. de Estructuras y Construcción por Antoni Marí
Ingeniería del Transporte y Territorio por Andrés López Pita
Ingeniería Computacional por Eugenio Oñate
Medio Ambiente y Sostenibilidad por Xavier Sánchez-Vila
Jornada I+D+i en Ingeniería Civil 2008 (1/2)
Accés obert
21 de nov. 2008
Conferencia "El CSIC y su relación con las Universidades" presentada por el Sr. Rafael Rodrigo, Presidente del Consejo Superior de Investigaciones Científicas durante la "Jornada I+D+i en Ingeniería Civil” realizada el día 21 de noviembre en la Sala de Actos de la Escuela de Ingenieros de Caminos, Canales y Puertos de Barcelona.
Presentació del Campus de la UPC a Terrassa
Accés obert
20 de nov. 2008
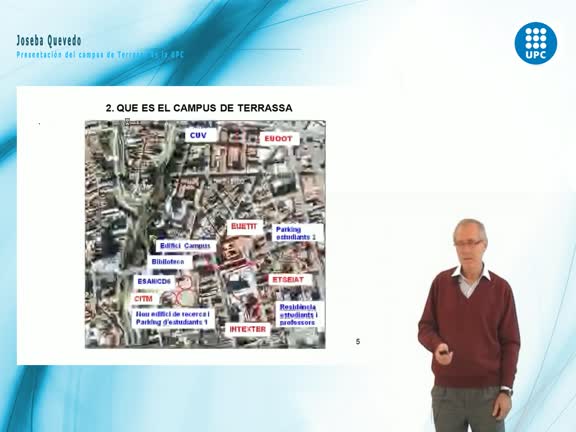
Presentació del Campus del la UPC a Terrassa per Joseba Quevedo.
Objetivos vivos. Paisajes sociales
Accés obert
19 de nov. 2008
Conferència impartida per l'arquitecte Emilio Tuñón a la Sala d'actes de l'ETSAB el 19 de novembre de 2008 per l' assignatura Projectes V-VI matí, Quadrimestre de tardor - Càtedra Blanca. Presentació a càrrec de Carlos Ferrater, Director de Càtedra Blanca i responsable de l'assignatura.
A simulation-based algorithm to predict time-dependent structural realiability
Accés obert
19 de nov. 2008
L’Institut d’Estadística i Matemàtica Aplicada a l’Edificació (IEMAE) recull propostes en el sector de l’edificació sostenible de professors de diferents departaments de l’EPSEB de forma transversal i en aquest context dinamitza i dóna suport a l’activitat dels seus membres en l’àrea de l’Estadística i Matemàtica Aplicada orientades a noves metodologies i les seves aplicacions.
Dins del Seminari de l'Institut trobem la següent exposició en català a càrrec del Dr. Àngel A. Juan, del Departament de Matemàtica Aplicada I (EPSEB-UPC)
Dins del Seminari de l'Institut trobem la següent exposició en català a càrrec del Dr. Àngel A. Juan, del Departament de Matemàtica Aplicada I (EPSEB-UPC)
![Acte de graduació de la promoció 2007-08[2/3]](/uploads/pic/series/603cca2afde9b8357e4e4e67/video/603d3401fde9b8393e4319e2/210301225340.jpg)
![Acte de graduació de la promoció 2007-08 [3/3]](/uploads/pic/series/603cca2afde9b8357e4e4e67/video/603d33fcfde9b8363c5c9b34/210301225159.jpg)
Acte d'investidura Magister Honoris Causa del Dr. Jaume Pagès Fita. Curs Noether (2008-2009)
Accés obert
14 de nov. 2008
Acte d'investidura Magister Honoris Causa del Dr. Jaume Pagès Fita
