Sèrie: Àlgebra lineal
10 de maig 2010
Estudi de la diagonalitzabilitat d’una matriu 3x3 depenent d’un paràmetre
Accés obert
10 de maig 2010
Aquest exercici resolt fa l’estudi de quan una matriu tres per tres depenent d’un paràmetre real és diagonalitzable en funció dels valors del paràmetre
Exercici de producte escalar a C^3 en el qual es demana una base ortogonal d’un subespai junt amb la projecció d’un vector sobre el subespai i la distància mínima a aquest
Accés obert
10 de maig 2010
En aquest exercici de producte escalar a C^3 es demana una base ortogonal d’un subespai de dimensió 2 a més de la projecció ortogonal d’un vector sobre el subespai i de la distància mínima a aquest
Exercici de producte escalar a C^3 en el qual es determina el valor d’uns paràmetres per tal que l’expressió donada sigui un producte escalar
Accés obert
10 de maig 2010
Es tracta d’un exercici resolt típic en el qual es dóna una expressió amb dos paràmetres reals pels quals es demana el valor que faci que l’expressió sigui un producte escalar a C^3
![Exercici de producte escalar a R_3[x] amb determinació d’una base ortogonal d’un subespai de dimensió 3, càlcul de projecció ortogonal d’un polinomi , així com de la seva component ortogonal](/uploads/pic/series/604633ee9e8fe022dd15713d/video/604666929e8fe024b90bab56/210308191129.jpg)
Exercici de producte escalar a R_3[x] amb determinació d’una base ortogonal d’un subespai de dimensió 3, càlcul de projecció ortogonal d’un polinomi , així com de la seva component ortogonal
Accés obert
10 de maig 2010
Aquest exercici de producte escalar a R_3[x] donat per una integral del producte dels dos polinomis que es multipliquen), planteja en primer lloc el càlcul d’una base ortogonal d’un subespai generat per 3 vectors L.I., la determinació de la projecció d’un polinomi sobre aquest subespai i la seva component ortogonal
15 de jul. 2011
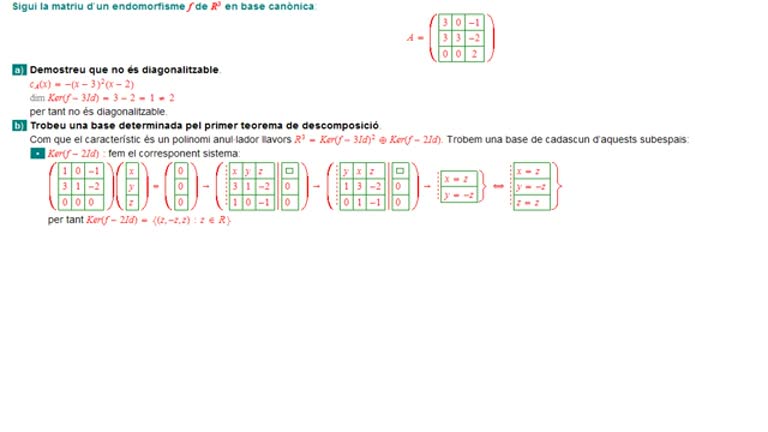
Exercici matriu diagonalitzable per blocs
Accés obert
15 de jul. 2011
Aquest exercici demana demostrar que una matriu no és diagonalitzable, a continuación es demana que es trobi una base determinada pel 1r. teorema descomposició i la matriu per blocs corresponent.
10 de maig 2010
Exercici sobre producte escalar a C^3 amb càlcul de l’ortogonal d’un subespai
Accés obert
10 de maig 2010
En aquest exercici es demana justificar que un suposat producte escalar a C^3 efectivament ho és. A continuació es demana calcular una base de l’ortogonal d’un subespai de dimensió 1 donat
per un generador
per un generador
21 de juny 2012
- ← Anterior
- 1 (current)
- Següent →
