Sèrie: FME Jornades temàtiques
21 de nov. 2019
Welcome. Workshop in honor of Alessio Figalli's "Doctor Honoris Causa at UPC"
Accés obert
21 de nov. 2019
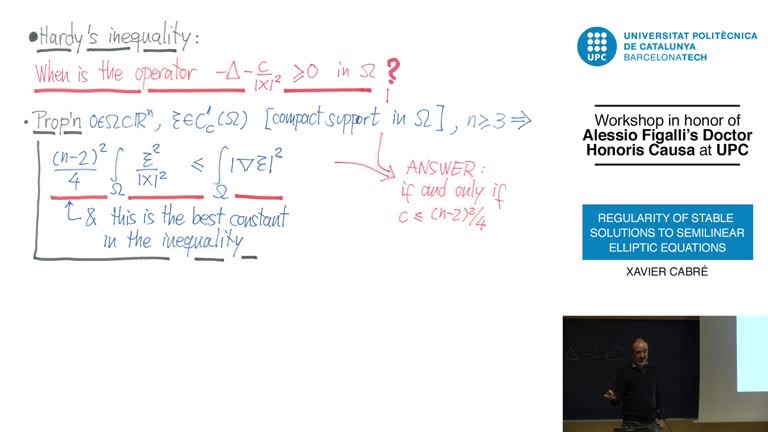
Regularity of stable solutions to semilinear elliptic equations. Workshop in honor of Alessio Figalli's "Doctor Honoris Causa at UPC"
Accés obert
21 de nov. 2019
The regularity of stable solutions to semilinear elliptic PDEs has been studied since the 1970's. In dimensions 10 and higher, there exist singular stable energy solutions. In this talk I will describe a recent work with Figalli, Ros-Oton, and Serra, where we prove that stable solutions are smooth up to the optimal dimension 9. This answers to a famous open problem posed by Brezis in the mid-nineties concerning the regularity of extremal solutions to Gelfand-type problems.
Round table. Workshop in honor of Alessio Figalli's "Doctor Honoris Causa at UPC"
Accés obert
21 de nov. 2019
Regularity of stable interfaces: from nonlocal to local. Workshop in honor of Alessio Figalli's "Doctor Honoris Causa at UPC"
Accés obert
21 de nov. 2019
I will describe recent results with Alessio Figalli on 1D symmetry of stable critical points of the Ginzburg-Landau functional associated to the half-Laplacian.
As we will discuss, an interesting feature of these functional is that it is asymptotic to the classical (local) perimeter, and thus their minimizers approximate sets of minimal perimeter.
As an application, we obtain the analogue for the half-Laplace of De Giorgi's conjecture in dimension four (a statement that is still open in the case of the Laplacian).
As we will discuss, an interesting feature of these functional is that it is asymptotic to the classical (local) perimeter, and thus their minimizers approximate sets of minimal perimeter.
As an application, we obtain the analogue for the half-Laplace of De Giorgi's conjecture in dimension four (a statement that is still open in the case of the Laplacian).
Nonlinear and nonlocal degenerate diffusions on bounded Domains. Workshop in honor of Alessio Figalli's "Doctor Honoris Causa at UPC"
Accés obert
21 de nov. 2019
Nonlinear diffusion models appear in several real world phenomena, ranging from physics, engineering and information theory to life sciences and finance. This talk will be focussed on a series of recent papers in collaboration with A. Figalli, X. Ros Oton,Y. Sire and J. L. Vázquez. We develop a complete theory for a diffusion model of Porous Medium type, with different nonlocal operators and degenerate nonlinearities. After a brief summary of the main features of such theory, we will focus our attention on (sharp) boundary estimates, showing how the degeneracy of the nonlinearity together with the nonlocal character of the equation, may cause a surprising anomalous boundary behaviour.
Generic regularity in free boundary problems. Workshop in honor of Alessio Figalli's "Doctor Honoris Causa at UPC"
Accés obert
21 de nov. 2019
Free boundary problems are those described by PDE's that exhibit a priori unknown (free) interfaces or boundaries. They appear in Geometry, Physics, Probability, Biology, or Finance, and their study uses tools from PDE, Geometric Measure Theory, and Calculus of Variations. The goal of this talk is to present different free boundary problems, explain the main known results in this context, and give an overview of the current research and open problems. In particular, we will discuss a long-standing open question in the field which concerns the generic regularity of free boundaries, and present some new results in this direction.
Elliptic and parabolic equations of fractional nonlocal type. Workshop in honor of Alessio Figalli's "Doctor Honoris Causa at UPC"
Accés obert
21 de nov. 2019
After a light motivation to the world of nonlocal equations of fractional type, placed inside the general theory of PDES and diffusion, the talk will present some recent work on the existence and behaviour of solutions of nonlinear fractional elliptic and parabolic equations, mainly when posed in bounded domains. The boundary behaviour is carelly examined, since it offers many novelties.
Works in collaboration with Figalli, Caffarelli, Bonforte, Sire, and Gomez-Castro,... "
Works in collaboration with Figalli, Caffarelli, Bonforte, Sire, and Gomez-Castro,... "
7 de maig 2014
