Objectes multimèdia amb l’etiqueta: Equacions diferencials i integrals
Resultats de la cerca
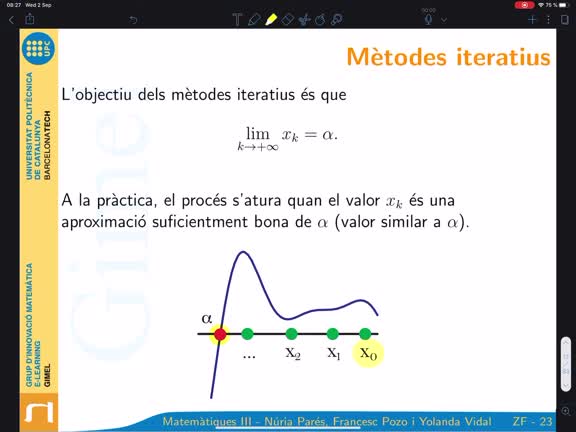
Zeros de funcions. Concepte mètode iteratiu
Accés obert
1 de gen. 2021
Vídeos docents de l'assignatura Càlcul (Q2) a l'Escola d'Enginyeria Barcelona de Est
Ordinary differential equations. Separable ODE
Accés obert
1 de gen. 2021
Vídeos docents de l'assignatura Càlcul (Q2) a l'Escola d'Enginyeria Barcelona de Est
Ordinary differential equations. Second order 1
Accés obert
1 de gen. 2021
Vídeos docents de l'assignatura Càlcul (Q2) a l'Escola d'Enginyeria Barcelona de Est
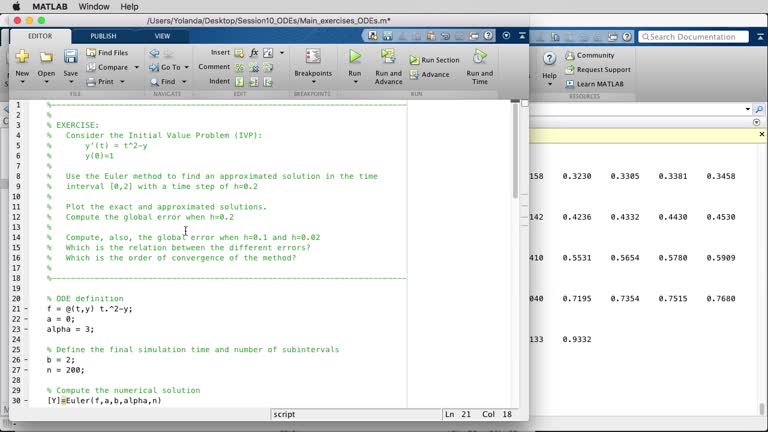
MATLAB. Ordinary differential equations
Accés obert
1 de gen. 2021
Vídeos docents de l'assignatura Càlcul (Q2) a l'Escola d'Enginyeria Barcelona de Est
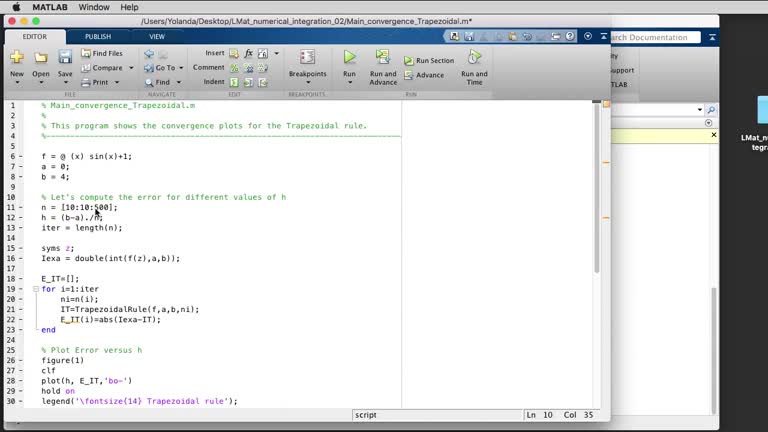
MATLAB. Numerical integration 02
Accés obert
1 de gen. 2021
Vídeos docents de l'assignatura Càlcul (Q2) a l'Escola d'Enginyeria Barcelona de Est
Ordinary differential equations. Second order
Accés obert
1 de gen. 2021
Vídeos docents de l'assignatura Càlcul (Q2) a l'Escola d'Enginyeria Barcelona de Est
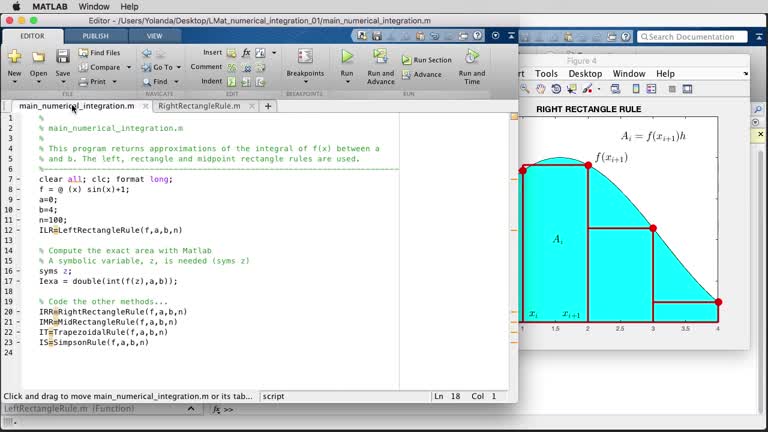
MATLAB. Numerical integration 01
Accés obert
1 de gen. 2021
Vídeos docents de l'assignatura Càlcul (Q2) a l'Escola d'Enginyeria Barcelona de Est
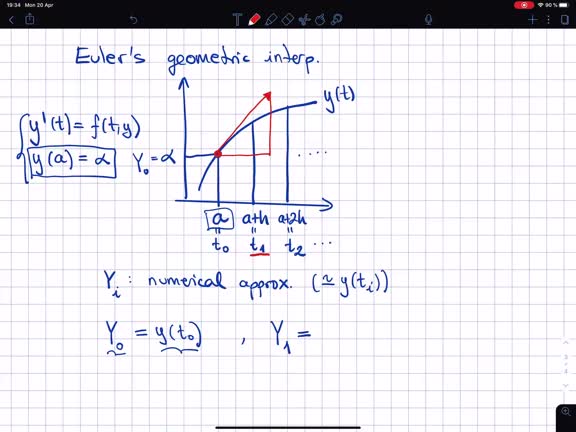
Ordinary differential equations. Numerical approximation
Accés obert
1 de gen. 2021
Vídeos docents de l'assignatura Càlcul (Q2) a l'Escola d'Enginyeria Barcelona de Est
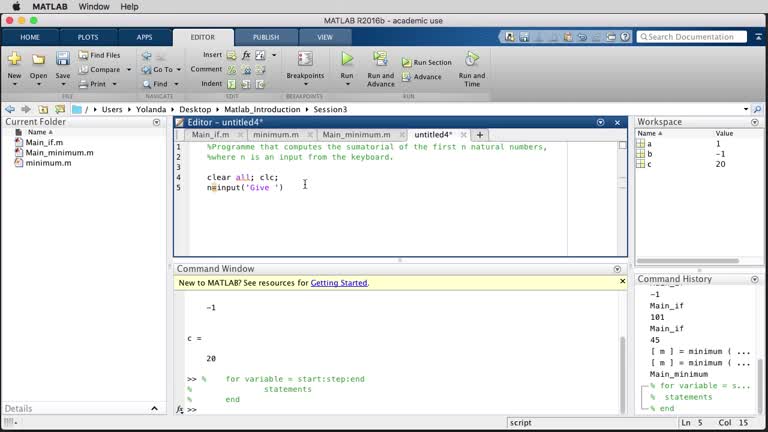
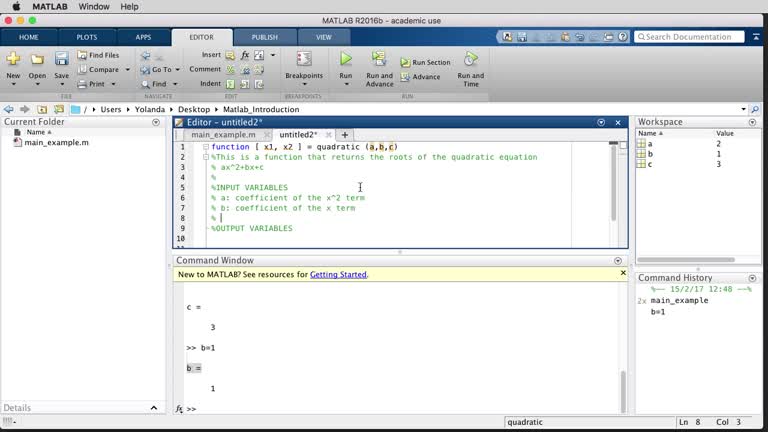
MATLAB. Introduction 03
Accés obert
1 de gen. 2021
Vídeos docents de l'assignatura Càlcul (Q2) a l'Escola d'Enginyeria Barcelona de Est
Ordinary differential equations. Motivation
Accés obert
1 de gen. 2021
Vídeos docents de l'assignatura Càlcul (Q2) a l'Escola d'Enginyeria Barcelona de Est
MATLAB. Introduction 02
Accés obert
1 de gen. 2021
Vídeos docents de l'assignatura Càlcul (Q2) a l'Escola d'Enginyeria Barcelona de Est
Ordinary differential equations. Introduction
Accés obert
1 de gen. 2021
Vídeos docents de l'assignatura Càlcul (Q2) a l'Escola d'Enginyeria Barcelona de Est