Objectes multimèdia amb l’etiqueta: Matemàtiques i estadística general
Resultats de la cerca
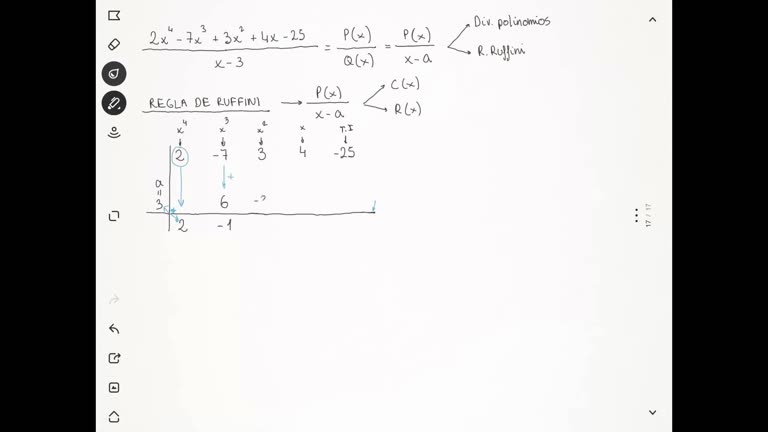
Tema 3 - Funcions elementals. Cálculo de un límite utilizando división de polinomios y Ruffini
Accés obert
29 de set. 2020
Curs de matemàtiques
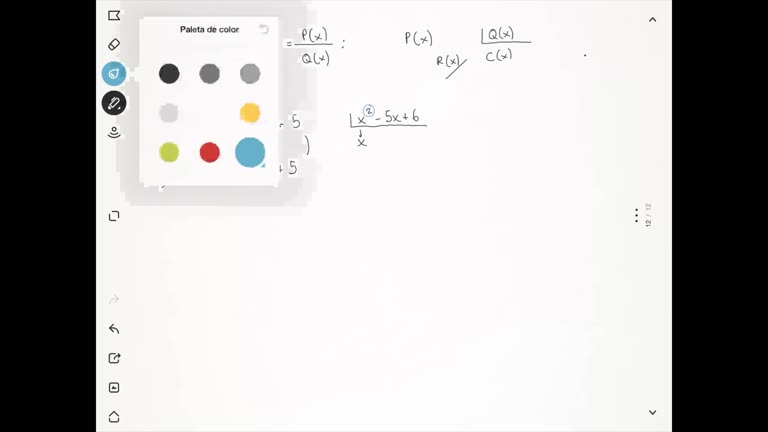
Tema 1 - Polinomis i trigonometria. División Polinomios
Accés obert
29 de set. 2020
Curs de matemàtiques
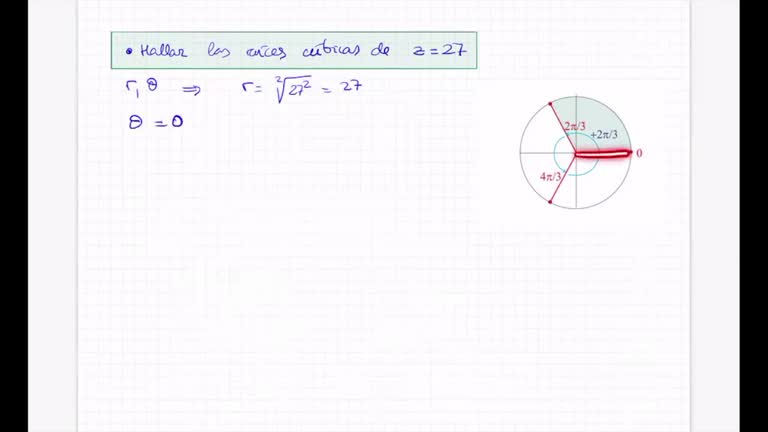
Tema 1 - Conjunts numèrics. 04 Complejos
Accés obert
1 de set. 2020
Vídeo docent de l'assignatura Càlcul de l'EEBE
Tema 1 - Conjunts numèrics. 03 Complejos
Accés obert
1 de set. 2020
Vídeo docent de l'assignatura Càlcul de l'EEBE
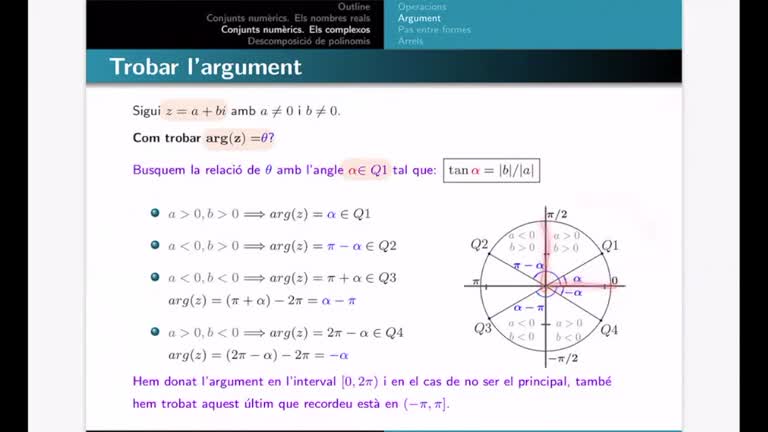
Tema 1 - Conjunts numèrics. 02 Argument
Accés obert
1 de set. 2020
Vídeo docent de l'assignatura Càlcul de l'EEBE