Objectes multimèdia amb l’etiqueta: Matemàtiques i estadística
Resultats de la cerca
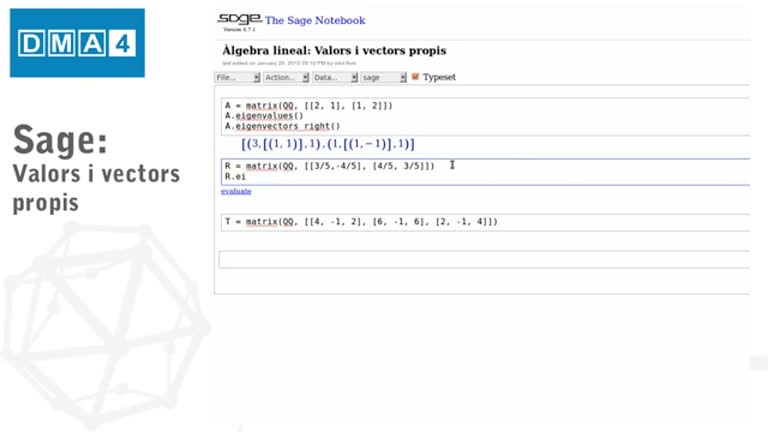
Fonaments matemàtics. Tutorial SAGE 9: Valors i vectors propis
Accés obert
16 d’abr. 2012
Tutorial d'introducció al programari SAGE. En aquest tutorial s'explica a l'alumne com calcular valors i vectors propis amb SAGE.
Fonaments matemàtics. Tutorial SAGE 8: Operacions entre matrius
Accés obert
16 d’abr. 2012
Tutorial d'introducció al programari SAGE. En aquest tutorial s'introdueix l'alumne a la realització d'operacions entre matrius amb SAGE.
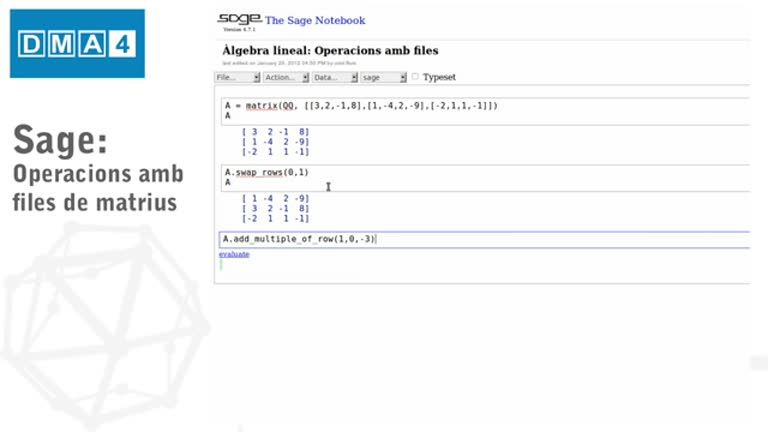
Fonaments matemàtics. Tutorial SAGE 7: Operacions amb files de matrius
Accés obert
16 d’abr. 2012
Tutorial d'introducció al programari SAGE. En aquest tutorial s'introdueix l'alumne a la realització d'operacions amb files de matrius amb SAGE.
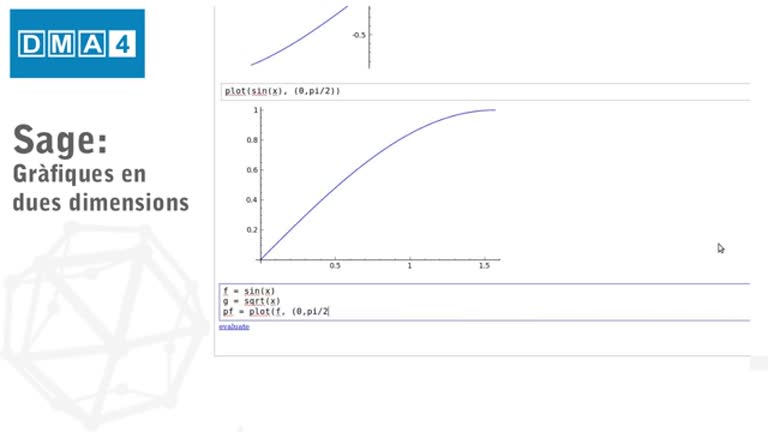
Fonaments matemàtics. Tutorial SAGE 6: Gràfiques en dues dimensions
Accés obert
16 d’abr. 2012
Tutorial d'introducció al programari SAGE
En aquest tutorial s'introdueix l'alumne a la realització de gràfiques en dues dimensions amb SAGE
En aquest tutorial s'introdueix l'alumne a la realització de gràfiques en dues dimensions amb SAGE
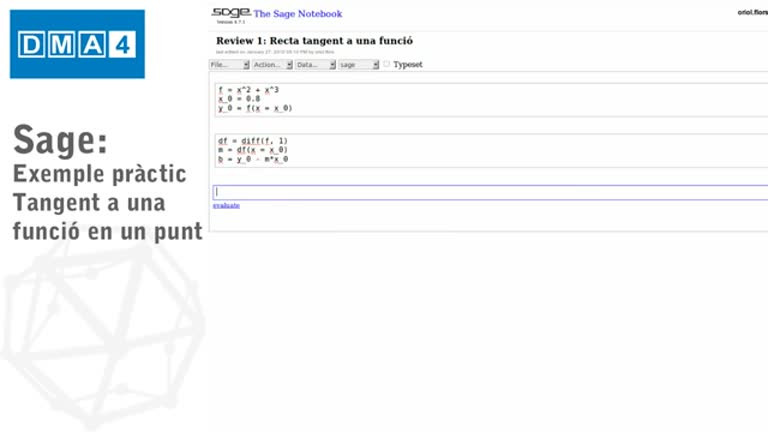
Fonaments matemàtics. Tutorial SAGE 5: Exemple pràctic. Tangent a una funció en un punt
Accés obert
16 d’abr. 2012
Tutorial d'introducció al programari SAGE. Exemple pràctic.
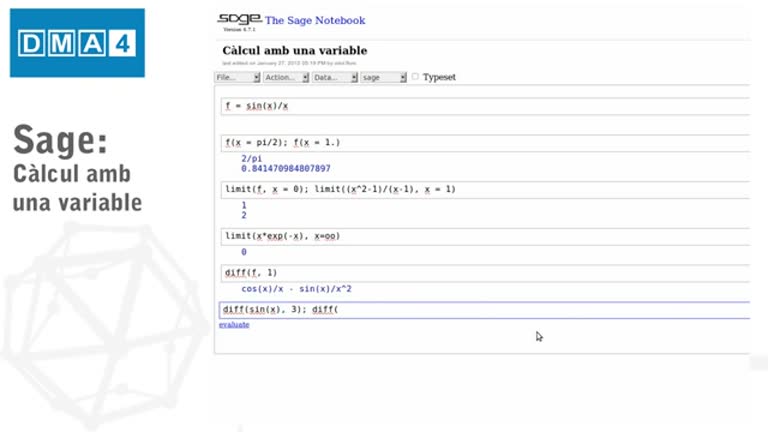
Fonaments matemàtics. Tutorial SAGE 4: Càlcul amb una variable
Accés obert
16 d’abr. 2012
Tutorial d'introducció al programari SAGE. En aquest tutorial s'introdueix l'alumne al càlcul de límits, derivades, primitives i integrals definides d'una funció en una variable real amb SAGE.
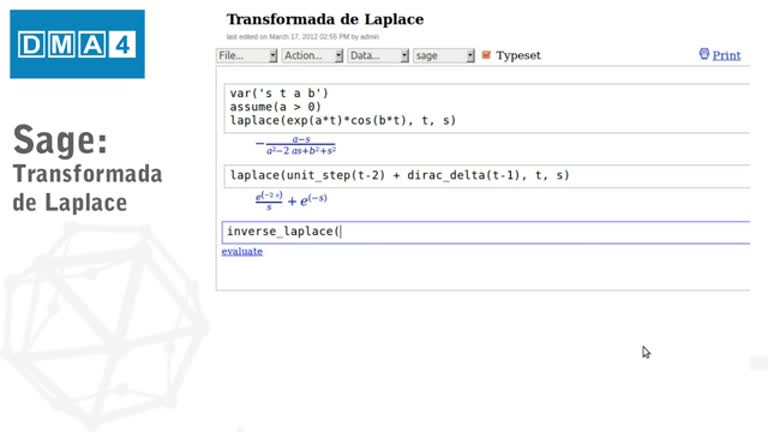
Fonaments matemàtics. Tutorial SAGE 3: Transformada de Laplace
Accés obert
16 d’abr. 2012
Tutorial d'introducció al programari SAGE. En aquest tutorial es treballa la transformada de Laplace en SAGE.
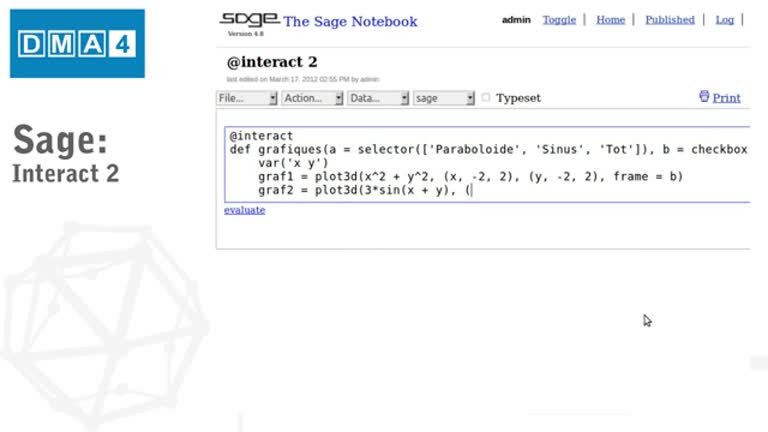
Fonaments matemàtics. Tutorial SAGE 2: Interact 2
Accés obert
16 d’abr. 2012
Tutorial d'introducció al programari SAGE. En aquest tutorial es proposa un segon exemple sobre l'entorn Interact, que permet crear applets amb SAGE.
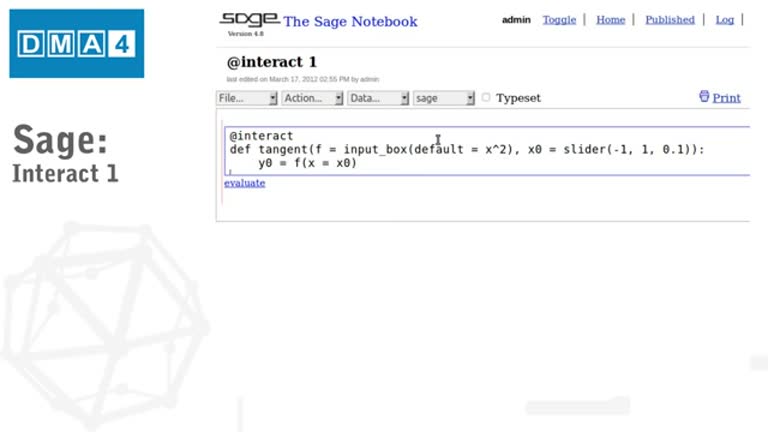
Fonaments matemàtics. Tutorial SAGE 1: Interact 1
Accés obert
16 d’abr. 2012
Tutorial d'introducció al programari SAGE. En aquest tutorial s'introdueix l'alumne a l'entorn Interact, que permet crear applets amb SAGE.
A new approach to the planetary N-Body Problem. Tutorial.
Accés obert
27 de març 2012
The planetary N-body problem.
Arnold's statement on the existence of maximal tori for the planetary problem (1963).
Classical Hamiltonian description (Delaunay, Poincare').
Degeneracies.
A brief history of the proof of Arnold's theorem.
A new approach to the planetary NBP (2011): Deprit's variables and Pinzari's regularization (the RPS variables).
Torsion. Full proof of Arnold's theorem (sketch).
Some consequences (measure estimates, Conley-Zehnder periodic orbits, Birkhoff normal forms).
Arnold's statement on the existence of maximal tori for the planetary problem (1963).
Classical Hamiltonian description (Delaunay, Poincare').
Degeneracies.
A brief history of the proof of Arnold's theorem.
A new approach to the planetary NBP (2011): Deprit's variables and Pinzari's regularization (the RPS variables).
Torsion. Full proof of Arnold's theorem (sketch).
Some consequences (measure estimates, Conley-Zehnder periodic orbits, Birkhoff normal forms).
A new approach to the planetary N-Body Problem. Tutorial.
Accés obert
26 de març 2012
The planetary N-body problem.
Arnold's statement on the existence of maximal tori for the planetary problem (1963).
Classical Hamiltonian description (Delaunay, Poincare').
Degeneracies.
A brief history of the proof of Arnold's theorem.
A new approach to the planetary NBP (2011): Deprit's variables and Pinzari's regularization (the RPS variables).
Torsion. Full proof of Arnold's theorem (sketch).
Some consequences (measure estimates, Conley-Zehnder periodic orbits, Birkhoff normal forms).
Arnold's statement on the existence of maximal tori for the planetary problem (1963).
Classical Hamiltonian description (Delaunay, Poincare').
Degeneracies.
A brief history of the proof of Arnold's theorem.
A new approach to the planetary NBP (2011): Deprit's variables and Pinzari's regularization (the RPS variables).
Torsion. Full proof of Arnold's theorem (sketch).
Some consequences (measure estimates, Conley-Zehnder periodic orbits, Birkhoff normal forms).
The Historical dispute between R. Fisher and J.Neyman. Jornada Fisher (Curs 2011-2012)
Accés obert
7 de març 2012