Objectes multimèdia amb l’etiqueta: Facultat de Matemàtiques i Estadística
Resultats de la cerca
Florence Nightingale: a role model in the 21st century. Lliçó inaugural Curs Nightingale (2020-2021)
Accés obert
14 d’oct. 2020
La professora Guadalupe Gómez obrirà el curs 2020-2021 de l'FME dedicat a Florence Nightingale
L'acte tindrà lloc dimecres 14 d'octubre 2020 a les 12.30 h a la sala d’actes de la Facultat.
Aforament limitat, caldrà inscripció prèvia
Florence Nightingale (1820 - 1910), estadística, reformadora social britànica i fundadora de la infermeria moderna. Va ser pionera en gràfics estadístics per representar visualment les dades i com a eina de comunicació. Va ser la primera dona admesa a la Royal Statistical Society així com membre honorària de l'American Statistical Association.
Florence tenia les idees molt clares i estava convençuda que el progrés era possible. Va destacar pel seu amor al raonament, per formular magistralment les preguntes adequades, va treballar sempre amb experts i va lluitar perquè els resultats fossin accessibles i convincents.
En paraules del seu biògraf Mark Bostridge," la societat té una responsabilitat col·lectiva per la salut de tots els seus membres".
L'acte tindrà lloc dimecres 14 d'octubre 2020 a les 12.30 h a la sala d’actes de la Facultat.
Aforament limitat, caldrà inscripció prèvia
Florence Nightingale (1820 - 1910), estadística, reformadora social britànica i fundadora de la infermeria moderna. Va ser pionera en gràfics estadístics per representar visualment les dades i com a eina de comunicació. Va ser la primera dona admesa a la Royal Statistical Society així com membre honorària de l'American Statistical Association.
Florence tenia les idees molt clares i estava convençuda que el progrés era possible. Va destacar pel seu amor al raonament, per formular magistralment les preguntes adequades, va treballar sempre amb experts i va lluitar perquè els resultats fossin accessibles i convincents.
En paraules del seu biògraf Mark Bostridge," la societat té una responsabilitat col·lectiva per la salut de tots els seus membres".
Acte d'investidura honoris causa del Dr. Alessio Figalli
Accés obert
13 de maig 2020
El divendres 22 de novembre, a les 11:30 h, a l’Auditori de l’edifici Vèrtex, va tenir lloc l’acte d’investidura del professor Alessio Figalli com a doctor honoris causa de la Universitat Politècnica de Catalunya · BarcelonaTech (UPC), a proposta de la Facultat de Matemàtiques i Estadística (FME).
Alessio Figalli és professor de l’ETH Zurich i un dels matemàtics internacionals més rellevants de l’actualitat, guardonat amb la medalla Fields 2018. El professor i investigador ICREA Xavier Cabré, del Departament de Matemàtiques de la UPC, ha exercit de padrí durant l’acte d’investidura.
Alessio Figalli és professor de l’ETH Zurich i un dels matemàtics internacionals més rellevants de l’actualitat, guardonat amb la medalla Fields 2018. El professor i investigador ICREA Xavier Cabré, del Departament de Matemàtiques de la UPC, ha exercit de padrí durant l’acte d’investidura.
No renunciïs! Tria Matemàtiques + Música
Accés obert
2 de maig 2020
La doble titulació Matemàtiques i Música que impartiran conjuntament a partir del proper curs la Facultat de Matemàtiques i Estadística (FME) de la UPC i l’Escola Superior de Música de Catalunya (ESMUC) és la primera proposta educativa a Catalunya que permet compaginar ambdós estudis alhora. Neix de la necessitat de donar resposta a la demanda d’una part de l’estudiantat que, fins ara, havia de triar entre una titulació o l’altra. Naila, Víctor i Laura t’expliquen en aquest vídeo les raons per estudiar aquests estudis.
Contribucions de Maryam Mirzakhani en dinàmica i geometria. Curs Fourier (2019-2020)
Accés obert
11 de març 2020
La conferència, accessible a una audiència general, traslladarà la rellevància i elegància d'algunes idees de Maryam Mirzakhani en l'estudi de les superfícies de Riemann i els seus espais de moduli, combinant conceptes de dinàmica i de geometria.
Remember Maryam Mirzakhani: una mirada col·lectiva. Curs Fourier (2019-2020)
Accés obert
12 de febr. 2020
17 plafons, 17 mirades: 17 professores del Departament de Matemàtiques de la UPC presenten cadascun dels plafons de l’exposició REMEMBER MARYAM MIRZAKHANI (vegeu díptic).
Alessio Figalli, doctor 'honoris causa' per la UPC
Accés obert
22 de nov. 2019
Alessio Figalli, doctor 'honoris causa' per la UPC, explica en aquesta entrevista el paper de les Matemàtiques en el desenvolupament de la tecnologia.
El matemàtic italià Alessio Figalli, professor de l’ETH Zurich i un dels matemàtics internacionals més rellevants de l’actualitat, ha estat investit, el 22 de novembre a Barcelona, doctor ‘honoris causa’ per la UPC, a proposta de la Facultat de Matemàtiques i Estadística (FME). En aquesta entrevista, el catedràtic explica el paper de les Matemàtiques en el desenvolupament de la tecnologia.
El matemàtic italià Alessio Figalli, professor de l’ETH Zurich i un dels matemàtics internacionals més rellevants de l’actualitat, ha estat investit, el 22 de novembre a Barcelona, doctor ‘honoris causa’ per la UPC, a proposta de la Facultat de Matemàtiques i Estadística (FME). En aquesta entrevista, el catedràtic explica el paper de les Matemàtiques en el desenvolupament de la tecnologia.
Welcome. Workshop in honor of Alessio Figalli's "Doctor Honoris Causa at UPC"
Accés obert
21 de nov. 2019
Round table. Workshop in honor of Alessio Figalli's "Doctor Honoris Causa at UPC"
Accés obert
21 de nov. 2019
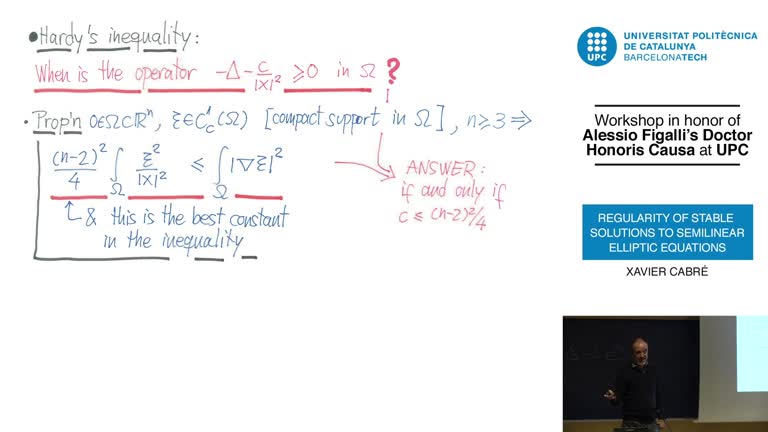
Regularity of stable solutions to semilinear elliptic equations. Workshop in honor of Alessio Figalli's "Doctor Honoris Causa at UPC"
Accés obert
21 de nov. 2019
The regularity of stable solutions to semilinear elliptic PDEs has been studied since the 1970's. In dimensions 10 and higher, there exist singular stable energy solutions. In this talk I will describe a recent work with Figalli, Ros-Oton, and Serra, where we prove that stable solutions are smooth up to the optimal dimension 9. This answers to a famous open problem posed by Brezis in the mid-nineties concerning the regularity of extremal solutions to Gelfand-type problems.
Regularity of stable interfaces: from nonlocal to local. Workshop in honor of Alessio Figalli's "Doctor Honoris Causa at UPC"
Accés obert
21 de nov. 2019
I will describe recent results with Alessio Figalli on 1D symmetry of stable critical points of the Ginzburg-Landau functional associated to the half-Laplacian.
As we will discuss, an interesting feature of these functional is that it is asymptotic to the classical (local) perimeter, and thus their minimizers approximate sets of minimal perimeter.
As an application, we obtain the analogue for the half-Laplace of De Giorgi's conjecture in dimension four (a statement that is still open in the case of the Laplacian).
As we will discuss, an interesting feature of these functional is that it is asymptotic to the classical (local) perimeter, and thus their minimizers approximate sets of minimal perimeter.
As an application, we obtain the analogue for the half-Laplace of De Giorgi's conjecture in dimension four (a statement that is still open in the case of the Laplacian).
Nonlinear and nonlocal degenerate diffusions on bounded Domains. Workshop in honor of Alessio Figalli's "Doctor Honoris Causa at UPC"
Accés obert
21 de nov. 2019
Nonlinear diffusion models appear in several real world phenomena, ranging from physics, engineering and information theory to life sciences and finance. This talk will be focussed on a series of recent papers in collaboration with A. Figalli, X. Ros Oton,Y. Sire and J. L. Vázquez. We develop a complete theory for a diffusion model of Porous Medium type, with different nonlocal operators and degenerate nonlinearities. After a brief summary of the main features of such theory, we will focus our attention on (sharp) boundary estimates, showing how the degeneracy of the nonlinearity together with the nonlocal character of the equation, may cause a surprising anomalous boundary behaviour.
