Objectes multimèdia amb l’etiqueta: Facultat de Matemàtiques i Estadística
Resultats de la cerca
La quarta dimensió Hipercubs: 70 anys de la pintura Corpus Hypercubus de Salvador Dalí (27 de novembre 2024)
Accés obert
27 de nov. 2024
3 Conferències i mostra d'art matemàtic. Organitzat per UPCArts amb la col·laboració de l'FME.
Ramanujan i l'infinit: de les particions a la funció tau. Lliçó inaugural Curs Ramanujan (2024-2025)
Accés obert
6 de nov. 2024
Dimecres 16 d'octubre a les 12.30 h a la sala d’actes de la Facultat tindrà lloc l'acte inaugural del curs, que enguany es dedica al matemàtic Srinivasa Ramanujan.
Acte d'inauguració del curs FME 2024-2025 amb lliçó inaugural de la professora Pilar Bayer (UB).
Foto: Marcel·lí Bayer, 2022
L’obertura del curs comptarà amb la presència de Pilar Bayer Isant, catedràtica emèrita d’Àlgebra de la Universitat de Barcelona, que impartirà la lliçó inaugural “Ramanujan i l'infinit: de les particions a la funció tau”.
Programa de l'acte:
Benvinguda a càrrec Jordi Guàrdia, degà de l'FME. Presentació de les activitats Ramanujan FME 2024-2025.
Lliçó inaugural a càrrec de la professora Pilar Bayer. "Ramanujan i l'infinit: de les particions a la funció tau”. Presentació a càrrec del professor Sebastià Xambó.
Lliurament del premi Carme Torras – Ailylabs a les millors estudiantes dels primers dos cursos del grau en Matemàtiques i del grau en Estadística UB-UPC.
Reconeixement a PDI i PAS vinculat a l’FME que s’han jubilat en el darrer curs
Reconeixement a membres del PAS a més de 25 anys de trajectòria professional vinculada a l’FME.
Cloenda a càrrec de Miquel Soriano, vicerector de PDI de la UPC.
Himne universitari Gaudeamus amb el Cor Ol·lari de l’FME.
Acte d'inauguració del curs FME 2024-2025 amb lliçó inaugural de la professora Pilar Bayer (UB).
Foto: Marcel·lí Bayer, 2022
L’obertura del curs comptarà amb la presència de Pilar Bayer Isant, catedràtica emèrita d’Àlgebra de la Universitat de Barcelona, que impartirà la lliçó inaugural “Ramanujan i l'infinit: de les particions a la funció tau”.
Programa de l'acte:
Benvinguda a càrrec Jordi Guàrdia, degà de l'FME. Presentació de les activitats Ramanujan FME 2024-2025.
Lliçó inaugural a càrrec de la professora Pilar Bayer. "Ramanujan i l'infinit: de les particions a la funció tau”. Presentació a càrrec del professor Sebastià Xambó.
Lliurament del premi Carme Torras – Ailylabs a les millors estudiantes dels primers dos cursos del grau en Matemàtiques i del grau en Estadística UB-UPC.
Reconeixement a PDI i PAS vinculat a l’FME que s’han jubilat en el darrer curs
Reconeixement a membres del PAS a més de 25 anys de trajectòria professional vinculada a l’FME.
Cloenda a càrrec de Miquel Soriano, vicerector de PDI de la UPC.
Himne universitari Gaudeamus amb el Cor Ol·lari de l’FME.
Análisis de Datos Longitudinales
Accés obert
4 de juny 2024
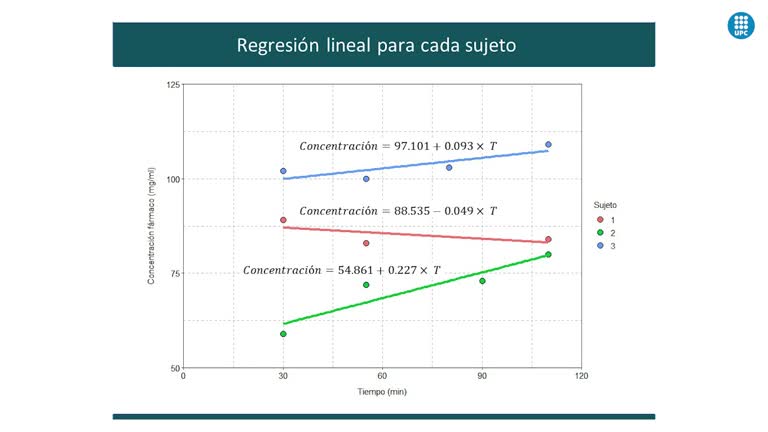
Los modelos estadísticos, como la regresión múltiple, relacionan una variable respuesta cuantitativa con varias variables explicativas. En estudios longitudinales, se observan sujetos a lo largo del tiempo, requiriendo técnicas estadísticas específicas debido a la correlación entre medidas intra-sujeto. Los modelos mixtos, que incluyen efectos fijos y aleatorios, son adecuados para capturar esta variabilidad y proporcionar estimaciones precisas.
Remembering George E.P. Box with: Tim Robinson (University of Wyoming) Curs Box 2023-2024
Accés obert
13 de maig 2024
Lean a l'aula: formalització a la docència
Accés obert
24 d’abr. 2024
L'assistent de demostracions LEAN és un llenguatge que ens permet escriure codi que conté definicions, enunciats i demostracions matemàtiques, i que no ens permet cometre errors. En els últims dos anys he estat utilitzant aquest sistema per introduir estudiants de diversos nivells al món de la formalització. Explicaré com ensenyem la geometria de Hilbert a estudiants de 4t d'ESO i Batxillerat fent servir aquest llenguatge, i com també l'hem fet servir amb estudiants de diferents cursos de matemàtiques a la UAB, sota el programa Lean a l'Aula. Veurem com s'interactua amb aquest sistema a la pràctica, i entre tots formalitzarem alguna demostració.
Publicació amb Quarto (Curs 2023-2024)
Accés obert
17 d’abr. 2024
Quarto és un sistema d'edició útil per a l'ensenyament i la publicació en matemàtiques basada en el llenguatge markdown. Aquest sistema permet la creació de llibres interactius amb suport per a codi executable (R, Python, Julia, etc..) , el que facilita la demostració de conceptes matemàtics d'una manera visual. A més, Quarto suporta una varietat de formats de sortida, incloent HTML per a publicació en línia i PDF per a distribució impresa, el que fa que sigui una eina molt versàtil.
Observable (Curs 2023-2024)
Accés obert
13 de març 2024
Observable és una plataforma per a equips de científics de dades, que permet una exploració de dades més profunda i més ràpida. Aquesta plataforma és ideal per a la visualització interactiva de dades, i permet explorar i comprendre les dades de manera més efectiva. Amb el suport per a una gran varietat de biblioteques de JavaScript, Observable us pot ajudar a convertir les dades en informació útil.
Remembering George E.P. Box with: Lourdes Pozueta (AVANCEX+i) Curs Box 2023-2024
Accés obert
6 de març 2024
Llenguatge "Julia" (Curs 2023-2024)
Accés obert
21 de febr. 2024
Llenguatge "Julia", a càrrec de Pere Joan Giménez Febrer. Doctor en Telecomunicacions per la UPC i treballa en la tecnològica Genie Framework de Barcelona desenvolupant el paquet Genie de Julia.
Remembering George E.P. Box with: Bart De Ketelaere (KU Leuven) Curs Box 2023-2024
Accés obert
15 de febr. 2024












.png)