Sèrie: FME Jornades del matemàtic/a del curs
14 de febr. 2007
Euler y los infinitos (grandes y pequeños). Jornada Euler (Curs 2006-2007)
Accés obert
14 de febr. 2007
...) Esta conferencia tratará de poner de manifiesto que la “Introductio” más que un texto de matemáticas es en realidad una gran novela de amor: la de Euler y los infinitos. Una pasión que bien pudo sugerirle a Immanuel Kant su célebre categoría estética de lo sublime.
Euler y la Teoría de Números. Jornada Euler (Curs 2006-2007)
Accés obert
14 de febr. 2007
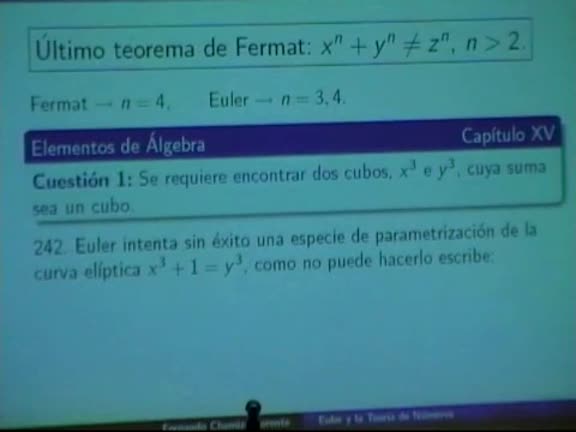
El gran Euler manifestó su genialidad en muchas áreas de las Matemáticas, entre ellas la teoría de números por la que tuvo un interés continuado a lo largo de su vida. El propósito de esta charla es ilustrar algunas de sus contribuciones principales a esta materia y reseñar la evolución posterior de los problemas que trató. La ingente producción de Euler obliga a una drástica selección que se regirá por cuatro de los grandes bloques en los que se pueden clasificar sus avances: divisibilidad, ecuaciones diofánticas, formas cuadráticas y distribución de los números primos.
15 de febr. 2006
Les disquisicions aritmètiques de Gauss. Jornada Gauss (Curs 2005-2006)
Accés obert
15 de febr. 2006
Aquesta conferència presenta un apropament a l’obra Disquisicions
aritmètiques, que C. F. Gauss publicà l’any 1801, quan comptava
24 anys. En una primera part, de caire històric, s’exposen les
circumstàncies que van concórrer en la seva elaboració. En una
segona part s’ofereix una visió del seu contingut, acompanyada
d’algunes reflexions sobre la seva influència posterior.
aritmètiques, que C. F. Gauss publicà l’any 1801, quan comptava
24 anys. En una primera part, de caire històric, s’exposen les
circumstàncies que van concórrer en la seva elaboració. En una
segona part s’ofereix una visió del seu contingut, acompanyada
d’algunes reflexions sobre la seva influència posterior.
Johann Carl Friedrich Gauss. Jornada Gauss (Curs 2005-2006)
Accés obert
15 de febr. 2006
Una apreciació de la figura científica de Gauss i el seu temps
Gauss y la estadística. Jornada Gauss (Curs 2005-2006)
Accés obert
15 de febr. 2006
Depués de considerar brevemente la polémica de Gauss con Legendre
a propósito de la autoría del método de los mínimos cuadrados,
se hace una exposición de dicho método, insistiendo en las
aportaciones estadísticas de Gauss al mismo, distinguiendo entre
la “Primera Aproximación de Gauss” (1809), en que supone la normalidad
de los errores de observación y la “Segunda Aproximación
de Gauss” (1821), en que restringe la clase de estimadores a las funciones
lineales de las observaciones y suprime la normalidad de los
errores. En la primera aproximación, el tratamiento es inferencial,
en la segunda es un tratamiento de Teoría de la Decisión.
a propósito de la autoría del método de los mínimos cuadrados,
se hace una exposición de dicho método, insistiendo en las
aportaciones estadísticas de Gauss al mismo, distinguiendo entre
la “Primera Aproximación de Gauss” (1809), en que supone la normalidad
de los errores de observación y la “Segunda Aproximación
de Gauss” (1821), en que restringe la clase de estimadores a las funciones
lineales de las observaciones y suprime la normalidad de los
errores. En la primera aproximación, el tratamiento es inferencial,
en la segunda es un tratamiento de Teoría de la Decisión.
Gauss i la geometria. Jornada Gauss (Curs 2005-2006)
Accés obert
15 de febr. 2006
Descripció dels principals treballs de Gauss sobre geometria i les seves repercussions posteriors.
Gauss i els polígons. Jornada Gauss (Curs 2005-2006)
Accés obert
15 de febr. 2006
Per copsar el llegat de Gauss, cal tenir en compte què
va fer, naturalment, però també què va deixar als altres per fer.
En aquest article expositiu, mostrem aquest fet en el cas de la
constructibilitat amb regle i compàs dels polígons regulars a la
circumferència i a la lemniscata. Gauss va provar (1796) que el
polígon regular de n costats es pot construir amb regle i compàs
si els factors primers senars de n són primers de Fermat diferents.
També va conjecturar que aquesta condició era necessària, la qual
cosa fou demostrada per Wantzel el 1836. Una nota “insinuant” a
les seves Disquisitiones Mathematicae va propiciar que Abel trobés
(1828) el mateix resultat per al cas dels polígons regulars de la
lemniscata; en aquest cas, el recíproc fou provat per Rosen el 1981.
va fer, naturalment, però també què va deixar als altres per fer.
En aquest article expositiu, mostrem aquest fet en el cas de la
constructibilitat amb regle i compàs dels polígons regulars a la
circumferència i a la lemniscata. Gauss va provar (1796) que el
polígon regular de n costats es pot construir amb regle i compàs
si els factors primers senars de n són primers de Fermat diferents.
També va conjecturar que aquesta condició era necessària, la qual
cosa fou demostrada per Wantzel el 1836. Una nota “insinuant” a
les seves Disquisitiones Mathematicae va propiciar que Abel trobés
(1828) el mateix resultat per al cas dels polígons regulars de la
lemniscata; en aquest cas, el recíproc fou provat per Rosen el 1981.
9 de febr. 2005
L'equació d'Einstein de la relativitat general i la seva relació amb l'equació d'ona. Jornada Einstein (Curs 2004-2005)
Accés obert
9 de febr. 2005
"La conferència tracta els punts següents: les nocions de relativitat especial a l’espai de Minkowski; els fonaments de la relativitat general i equació d’Einstein; la relació de l’equació d’Einstein amb l’equació d’ona clàssica; i breus pinzellades de la meva recerca personal en aquest camp".
Geometría de Lorentz : de lenguaje a herramienta básica en relatividad general. Jornada Einstein (Curs 2004-2005)
Accés obert
9 de febr. 2005
"Desde que Einstein extendió el espacio-tiempo de Lorentz-Minkowski a una variedad de Lorentz curvada para modelar campos gravitatorios no nulos, la Geometría de Lorentz, en su aspecto local, ha sido la herramienta fundamental en esta rama de la Física..."
Einstein y las teorías de campos unificados. Jornada Einstein (Curs 2004-2005)
Accés obert
9 de febr. 2005
La conferencia explica la unificació de la teoria del camp de la gravitació i la teoria de camp electromagnètic "Sería un gran paso adelante unificar en un simple esquema los campos gravitatorios y electromagnéticos. Sería un remate satisfactorio de la Época de la física teórica comenzada por Faraday y Maxwell" [Einstein, 1920].
Del efecto fotoeléctrico (1905) a la condensación de Bose-Einstein (1925) : un curioso ejemplo de simbiosis en el desarrollo de teorías físicas. Jornada Einstein (Curs 2004-2005)
Accés obert
9 de febr. 2005
La conferencia iene como objetivo analizar por una parte el papel jugado por las ideas estadísticas en el nacimiento y desarrollo de las primeras ideas cuánticas. Pero, además, trataremos de poner de manifiesto que la propia física estadística recibió fuertes impulsos en su desarrollo, como consecuencia de su participación en la aventura cuántica
29 de gen. 2004
Poincaré, pensador de la matemática. Jornada Poincaré (Curs 2003-2004)
Accés obert
29 de gen. 2004
Hay matemáticos que parecen hacer, únicamente, matemática porque no divulgan su pensamiento acerca de lo que hacen -caso Hermite-. Poincaré piensa en torno a lo que hace y lo divulga, lo hace público. En ese pensar llega a la convicción de que hay principios regulativos como la inducción completa, la estructura de grupo, las nociones topológicas... que posibilitan la creación matemática, obra de la razón. Creación matemática ligada siempre a los problemas que plantea el conocimiento de la physis, no encerrada en torre de marfil.
