Intel·ligència artificial: on som, on anem i on podríem arribar (Contextualització de les Matemàtiques a les carreres tecnològiques de la UPC)
Accés obert
17 de nov. 2021
36
visualitzacions
Tetiana Klymchuk
És ben conegut que per aconseguir una major motivació i aprofitament de l’estudiantat, convé contextualitzar les ciències (matemàtiques, física,...) mitjançant aplicacions immediates a les disciplines de la carrera. En una primera fase el projecte es centrarà en les matemàtiques, per després tractar altres disciplines, tals com la Física. Per exemple, modelitzant matricialment problemes d’enginyeria i aplicant a continuació tècniques de càlcul matricial per al seu estudi i resolució.
Llicència: Reconocimiento-NoComercial-SinObraDerivada 3.0 España (CC BY-NC-ND 3.0 ES)
Vídeos de la mateixa sèrie
Intel·ligència artificial: on som, on anem i on podríem arribar (Contextualització de les Matemàtiques a les carreres tecnològiques de la UPC)
Accés obert
17 de nov. 2021
És ben conegut que per aconseguir una major motivació i aprofitament de l’estudiantat, convé contextualitzar les ciències (matemàtiques, física,...) mitjançant aplicacions immediates a les disciplines de la carrera. En una primera fase el projecte es centrarà en les matemàtiques, per després tractar altres disciplines, tals com la Física. Per exemple, modelitzant matricialment problemes d’enginyeria i aplicant a continuació tècniques de càlcul matricial per al seu estudi i resolució.
Criptografia: L’aritmètica dels nombres grans (Contextualització de les Matemàtiques a les carreres tecnològiques de la UPC)
Accés obert
27 de maig 2021
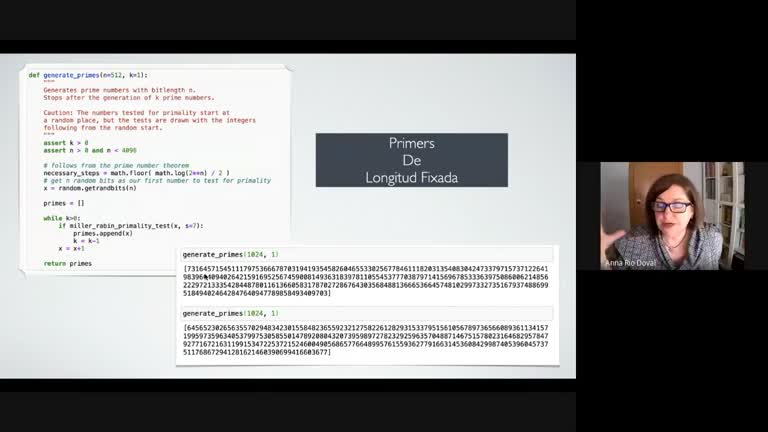
Les demandes computacionals dels nostres sistemes criptogràfics giren a l’entorn de l’aritmètica amb nombres enters grans, típicament de com a mínim 2048 bits (617 dígits decimals) si parlem de sistemes basats en la factorització d’enters i de com a mínim 256 bits (78 dígits decimals) si parlem de sistemes basats en el logaritme discret en corbes el·líptiques. En aquest context resultats matemàtics clàssics, com el teorema del nombre primer o la fita de Hasse conjecturada per Artin, proporcionen la base teòrica sobre la que es construeixen els algoritmes que fan funcionar les targetes digitals, els moneders de criptomonedes o multitud d’altres aplicacions de comunicació segura, signatura digital i protocols criptogràfics diversos. Així mateix, aquests algoritmes aritmètics segueixen sent peces fonamentals per a les noves propostes post-quàntiques basades en lattices o en isogènies de corbes supersingulars.
Probabilitats i teoria de la comunicació: codificació, caminades aleatòries en grafs i algorismes. (Contextualització de les Matemàtiques a les carreres tecnològiques de la UPC)
Accés obert
2 de des. 2020
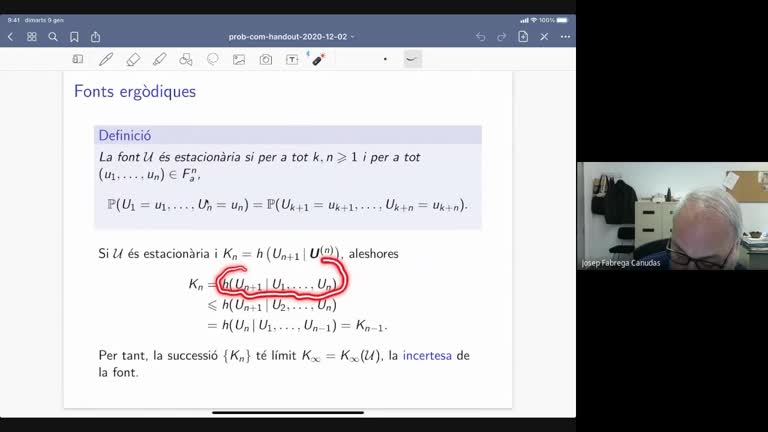
Es presentaran a nivell introductori alguns temes de les matemàtiques de les telecomunicacions i de la informació que es poden explicar en els currículums d'alguns dels nostres graus, com ara: taxes de codificació fiables, fonts de Markov i fonts ergòdiques, i camins aleatoris en grafs i xarxes elèctriques. Les probabilitats i les cadenes de Markov seran el nexe per recórrer aquests conceptes.
Matemàtiques animades. (Contextualització de les Matemàtiques a les carreres tecnològiques de la UPC)
Accés obert
16 d’oct. 2019
Les Matemàtiques de Google. (Contextualització de les Matemàtiques a les carreres tecnològiques de la UPC)
Accés obert
23 de maig 2018
Fluxos en xarxes. (Contextualització de les Matemàtiques a les carreres tecnològiques de la UPC)
Accés obert
24 d’abr. 2018
Fluxos en xarxes, a càrrec de Josep Ferrer Llop (Dept. Matemàtiques UPC)
Dimecres 25/04/2018
Aula 004 FME
12-13h30
Dimecres 25/04/2018
Aula 004 FME
12-13h30
Benvinguda - Parlaments (Contextualització de les Matemàtiques a les carreres tecnològiques de la UPC)
Accés obert
10 d’abr. 2018