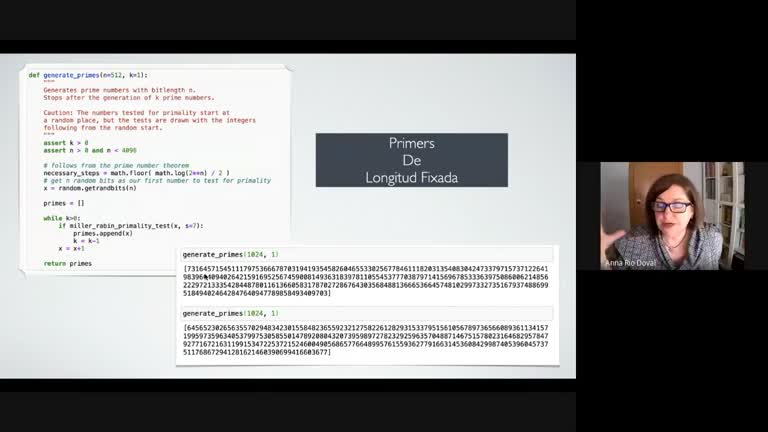
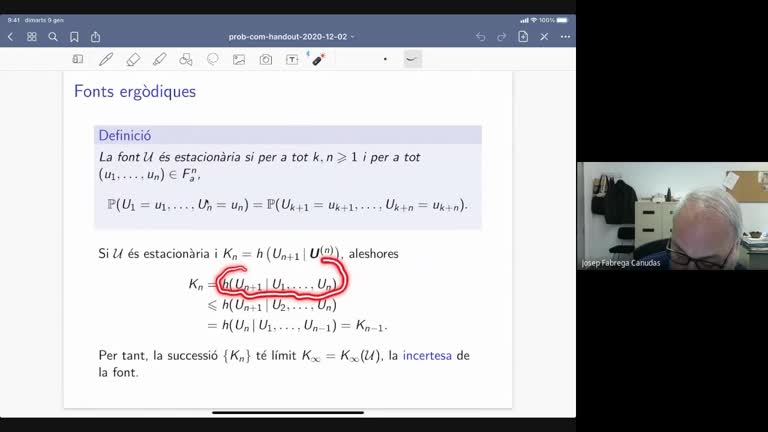
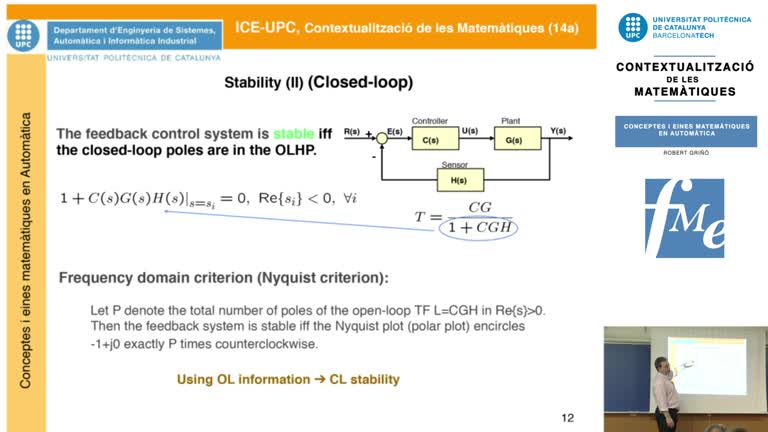
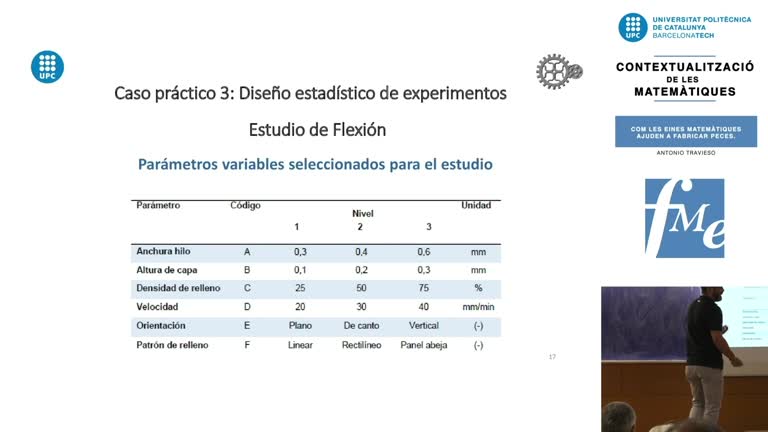
Les demandes computacionals dels nostres sistemes criptogràfics giren a l’entorn de l’aritmètica amb nombres enters grans, típicament de com a mínim 2048 bits (617 dígits decimals) si parlem de sistemes basats en la factorització d’enters i de com a mínim 256 bits (78 dígits decimals) si parlem de sistemes basats en el logaritme discret en corbes el·líptiques. En aquest context resultats matemàtics clàssics, com el teorema del nombre primer o la fita de Hasse conjecturada per Artin, proporcionen la base teòrica sobre la que es construeixen els algoritmes que fan funcionar les targetes digitals, els moneders de criptomonedes o multitud d’altres aplicacions de comunicació segura, signatura digital i protocols criptogràfics diversos. Així mateix, aquests algoritmes aritmètics segueixen sent peces fonamentals per a les noves propostes post-quàntiques basades en lattices o en isogènies de corbes supersingulars.
Vídeos de la mateixa sèrie
Intel·ligència artificial: on som, on anem i on podríem arribar (Contextualització de les Matemàtiques a les carreres tecnològiques de la UPC)
Criptografia: L’aritmètica dels nombres grans (Contextualització de les Matemàtiques a les carreres tecnològiques de la UPC)
Probabilitats i teoria de la comunicació: codificació, caminades aleatòries en grafs i algorismes. (Contextualització de les Matemàtiques a les carreres tecnològiques de la UPC)
Matemàtiques animades. (Contextualització de les Matemàtiques a les carreres tecnològiques de la UPC)
Les Matemàtiques de Google. (Contextualització de les Matemàtiques a les carreres tecnològiques de la UPC)
Fluxos en xarxes. (Contextualització de les Matemàtiques a les carreres tecnològiques de la UPC)
Dimecres 25/04/2018
Aula 004 FME
12-13h30