Perspectiva cónica (CO), ejercicio: Tetraedro, método de las prolongaciones
Accés obert
1 de febr. 2016
3
visualitzacions
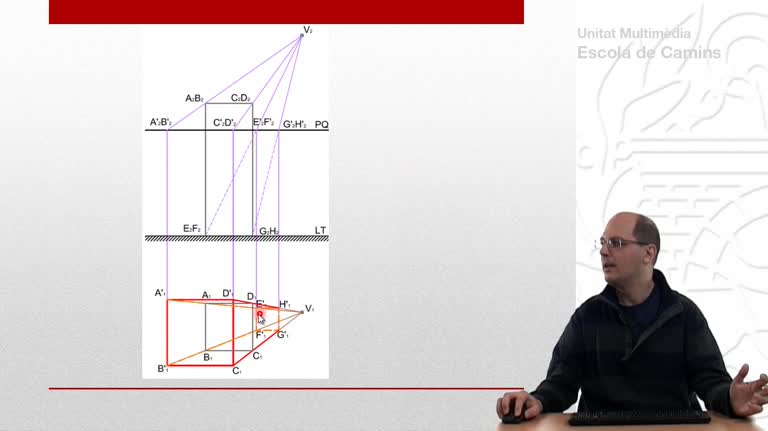
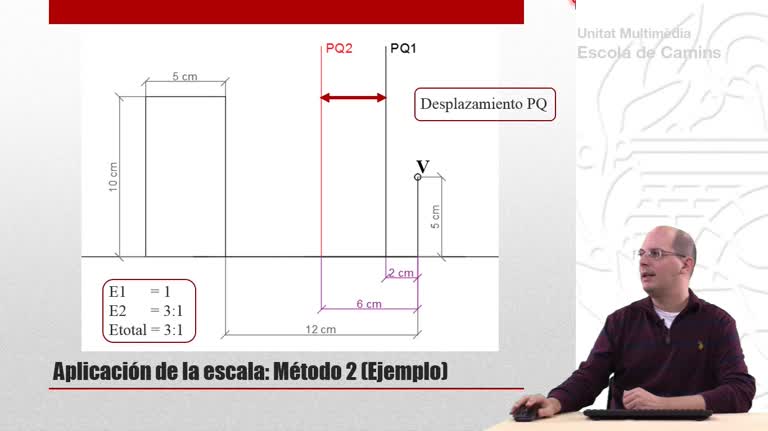
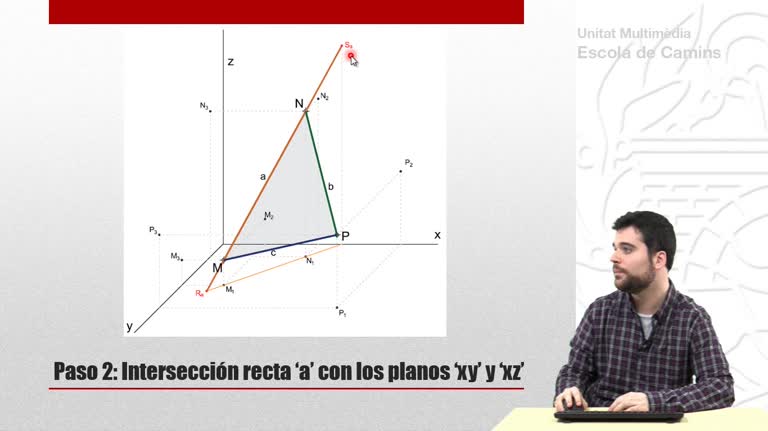
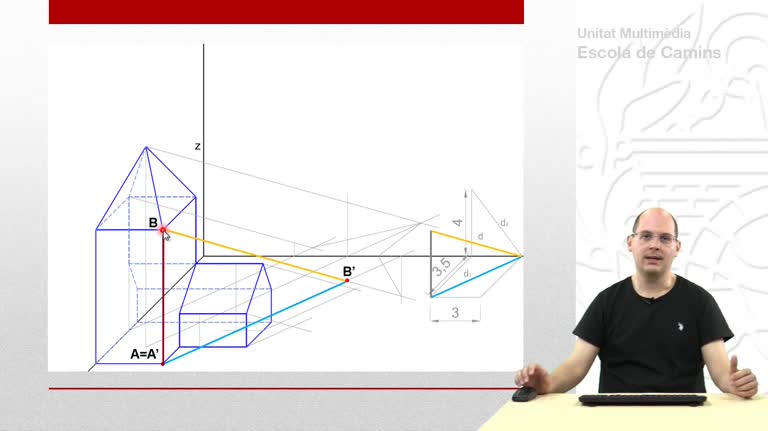
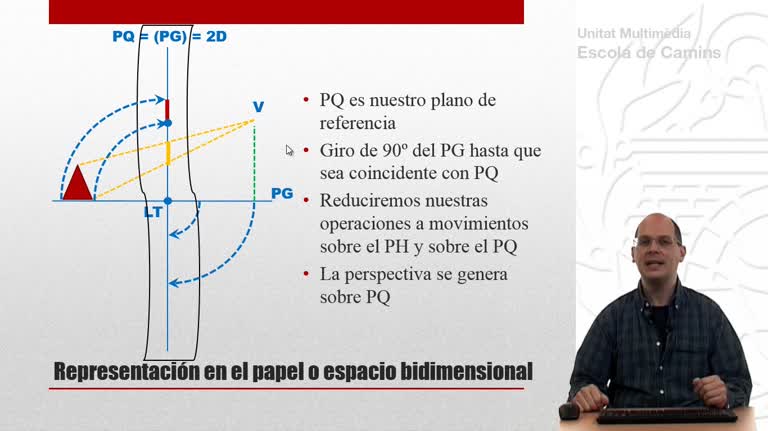
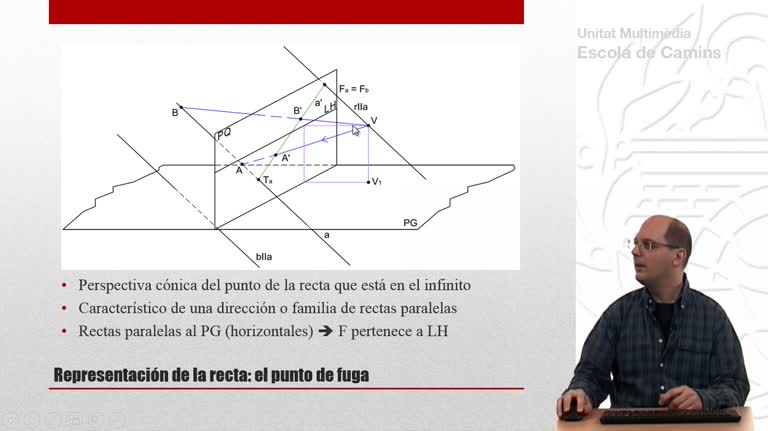
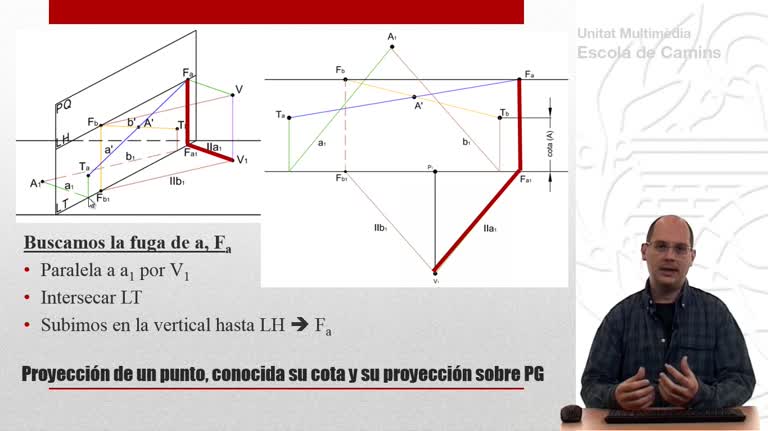
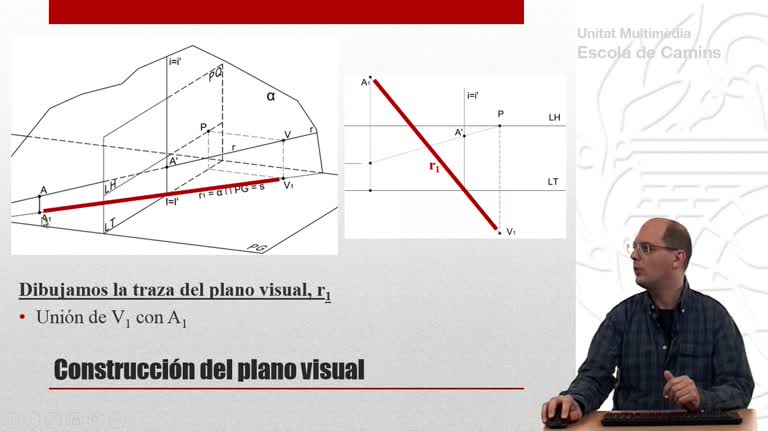
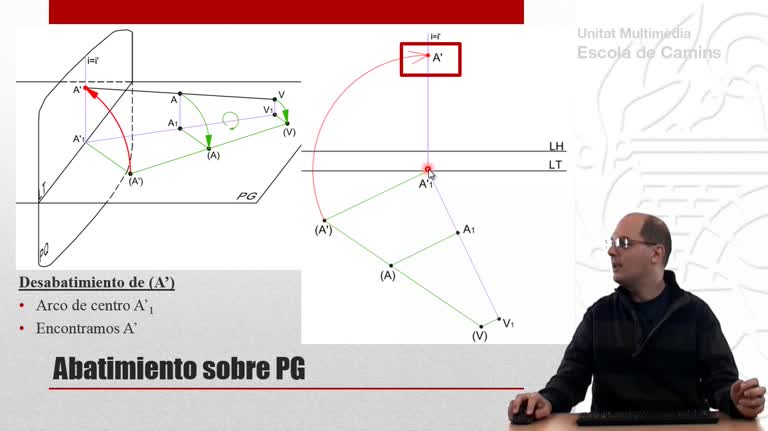
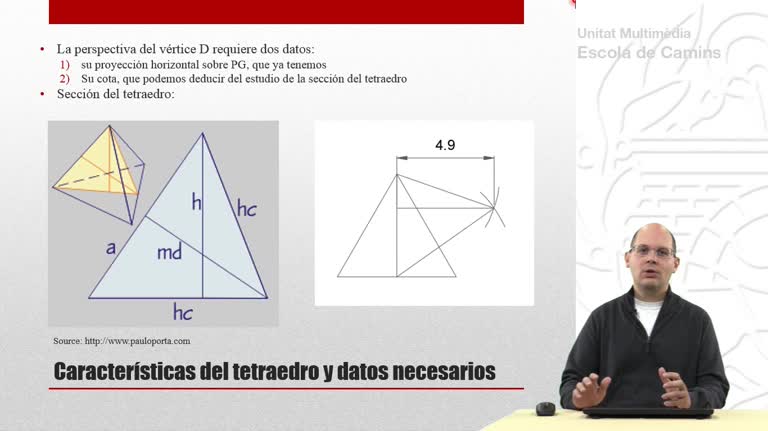
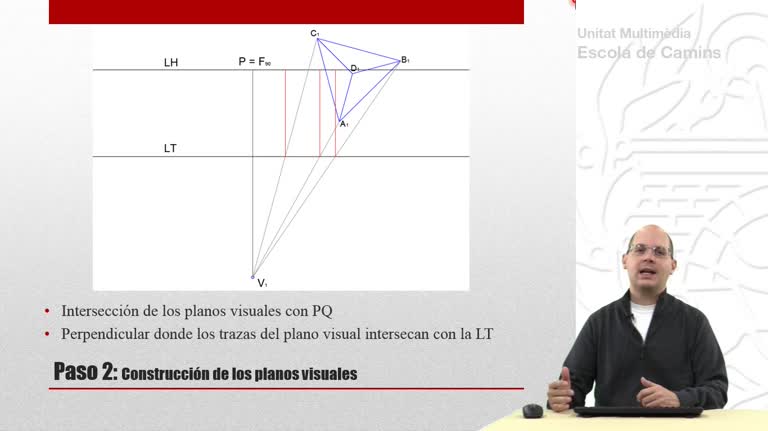
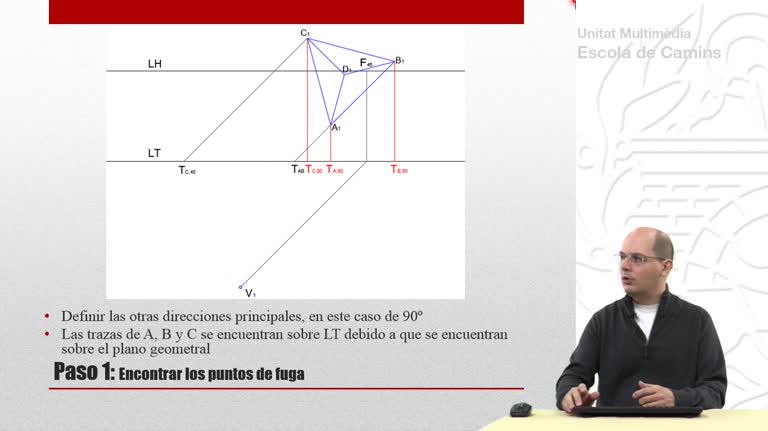
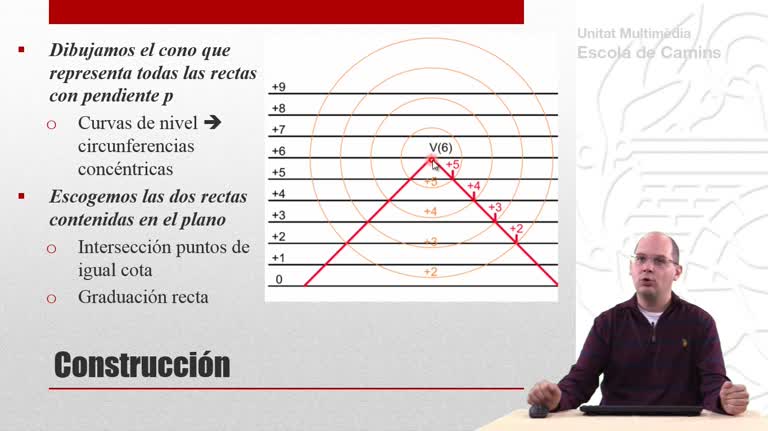
Perspectiva cónica de un tetraedro que descansa sobre el plano geometral. En esta primera parte se utiliza el método de las prolongaciones.
Llicència: Reconocimiento-NoComercial-SinObraDerivada 3.0 España (CC BY-NC-ND 3.0 ES)
Vídeos de la mateixa sèrie
Perspectiva cónica (CO), ejercicio: Tetraedro, cota del punto de vista nula
Accés obert
1 de febr. 2016
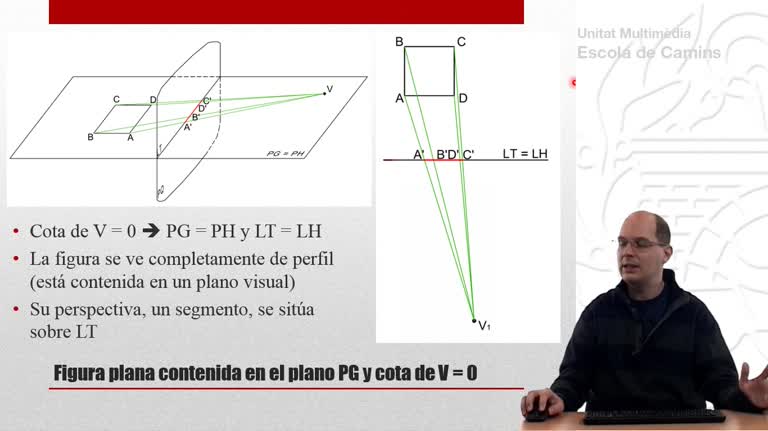
Perspectiva cónica de un tetraedro que descansa sobre el plano geometral. El punto de vista tiene cota nula, con lo cual la planta del tetraedro se ve de perfil.
Perspectiva cónica (CO), ejercicio: Tetraedro, rectas de punta y planos visuales
Accés obert
1 de febr. 2016
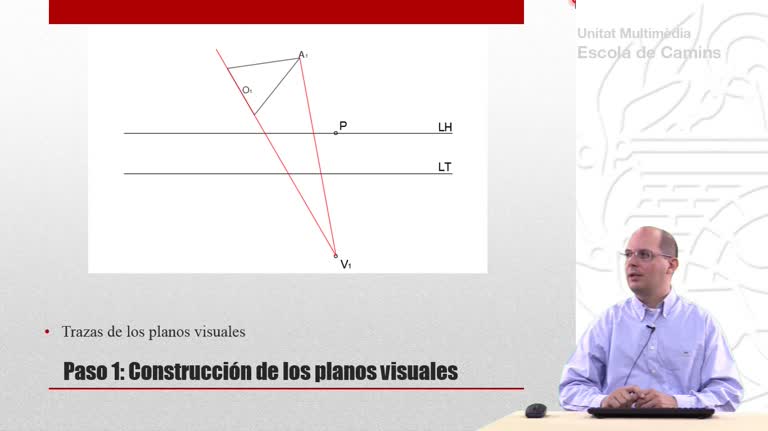
Perspectiva cónica de un tetraedro que descansa sobre el plano geometral. En esta segunda parte se utilizan planos visuales y rectas de punta.
Perspectiva cónica (CO), ejercicio: Tetraedro, método de las prolongaciones
Accés obert
1 de febr. 2016
Perspectiva cónica de un tetraedro que descansa sobre el plano geometral. En esta primera parte se utiliza el método de las prolongaciones.